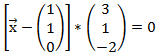Umrechnung Normalenform – Koordinatenform
Normalenform zur Koordinatenform
Um von der Normalenform zur Koordinatenform zu kommen muss man lediglich die Normalenform ausmultiplizieren.
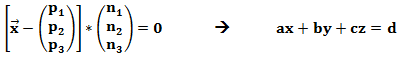
Das Ausmultiplizieren von Vektoren funktioniert genauso wie das normale Ausmultiplizieren.
![]()
Beispiel
Folgende Ebene ist in der Normalenform gegeben:
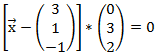
Um zu der Koordinatenform zu gelangen multiplizieren wir die Klammern aus:
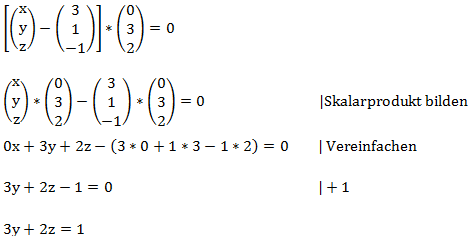
Das Ergebnis ist die Ebene in der Koordinatenform.
Unser Lernvideo zu : Umrechnung Normalenform – Koordinatenform
Koordinatenform zur Normalenform
Ebenfalls relativ einfach ist die Umrechnung von der Koordinatenform zu der Normalenform.
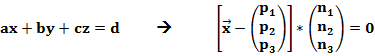
Beispiel
Gegeben ist eine Ebene in der Koordinatenform:
![]()
Wir lesen uns einfach den Normalenvektor von den Koeffizienten (3, 1 und -2) ab. Der Normalenvektor lautet:
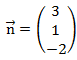
Jetzt benötigen wir nur noch einen Punkt, der die Koordinatengleichung erfüllt. Für diesen Punkt gibt es unendlich viele Möglichkeiten. Wir finden ihn, indem wir uns die x- und y-Koordinaten aussuchen und die dazugehörige z Koordinate ausrechnen. Manchmal ist es allerdings auch schneller kurz im Kopf zu überlegen mit welchen Werten die Gleichung erfüllt ist. Wir suchen uns aus:
![]()
Nun berechnen wir z indem wir x und y in die Gleichung einsetzen und nach z umformen:
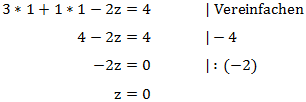
Unser Stützvektor lautet:
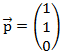
Damit sieht die Normalenform folgendermaßen aus: