Lineare Abhängigkeit
Vektoren sind linear Abhängig wenn sich ein Vektor durch die Kombination der anderen Vektoren darstellen lässt.
Zwei Vektoren sind linear abhängig, wenn sie in dieselbe Richtung weisen. Sie müssen also ein Vielfaches voneinander sein. Beispiele für linear abhängige Vektoren sind:

Der zweite Vektor lässt sich hier immer durch ein Vielfaches des Ersten abbilden. Wenn zwei Vektoren linear abhängig sind, kann man mit diesen beiden Vektoren keine Ebene beschreiben, da sie keine Ebene aufspannen können.
Nun schauen wir uns das Ganze mit drei Vektoren an. Drei Vektoren sind dann linear abhängig wenn sich ein Vektor durch die Kombination aus den beiden anderen darstellen lässt.
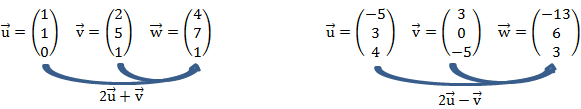
Wir sehen hier, dass sich der dritte Vektor aus den anderen beiden berechnen lässt. Der dritte Vektor liefert also keine neue Information und kann weggelassen werden. Alle Punkte im Koordinatensystem die durch die Kombination von ![]() ,
, ![]() und
und ![]() erreicht werden können, könne auch nur durch die Kombination von
erreicht werden können, könne auch nur durch die Kombination von ![]() und
und ![]() erreicht werden.
erreicht werden.
