Tabellarische Übersicht
Hier die wichtigsten Aufleitungen der Potenzfunktion, Wurzel, Exponentialfunktion und trigonometrischen Funktionen tabellarisch aufgeführt: * Diese Aufleitung gilt nur für den
Ausführliche InfosBei der Integralrechnung handelt es sich um die Umkehrung der Differentialrechnung. Das Ergebnis eines Integrals lässt sich als Fläche zwischen dem Graphen der Funktion, der x-Achse und den begrenzenden Parallelen zur y-Achse deuten.
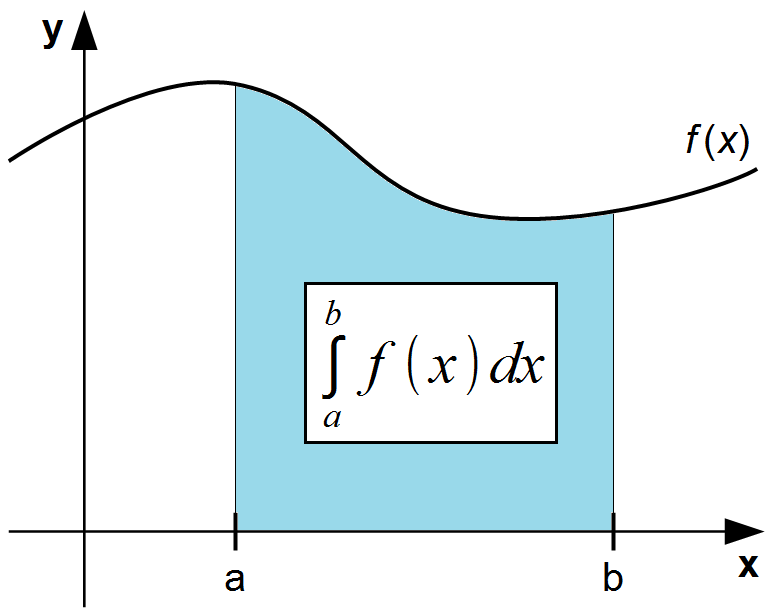
Die Berechnung selbst basiert auf der Überlegung, dass man sich die Fläche als ganz viele sehr schmale Rechtecke vorstellen kann, da es für Rechtecke ja sehr leicht ist die Fläche anzugeben. Auf diese Weise kommt man auch an Flächen unterhalb von nahezu beliebig komplexen Funktionsgraphen.
Die Integralrechnung ist ein zentraler Punkt der mathematischen Ausbildung in einer höheren Schule. Nahezu jedes Kind durchläuft in seinem Leben die Zeit, in dem es die Integralrechnung erlernt. Bei diesem mathematischen Problem geht es um die Berechnung von Flächen mit der Hilfe der Umkehrung der Differenzialrechnung. Das Integral ist die Fläche zwischen dem Graphen einer Funktion und der x-Achse innerhalb eines bestimmten Abschnittes. Richtig spannend ist die Volumenberechnung eines Körpers. Bis zu diesem Schritt ist allerdings das folgende Grundwissen notwendig.
Hier die wichtigsten Aufleitungen der Potenzfunktion, Wurzel, Exponentialfunktion und trigonometrischen Funktionen tabellarisch aufgeführt: * Diese Aufleitung gilt nur für den
Ausführliche InfosWir haben bereits gelernt, wie man die Fläche zwischen dem Graphen einer Funktion und der x-Achse bestimmen kann. Mit diesem
Ausführliche InfosBei der Integration ist zu prüfen, ob sich die berechnete Fäche vollständig auf einer Seite der x-Achse befindet. Sollte dies
Ausführliche InfosDie Substitutionsregel (Substitution heißt Ersetzung) bei der Integration kann als Gegenstück zur Kettenregel beim Ableiten gesehen werden. Auch hier liegt
Ausführliche InfosDie partielle Integration wird verwendet, wenn ein Produkt aufgeleitet werden soll, dessen Faktoren jeweils von x abhängig sind. Eine Abhängigkeit
Ausführliche InfosBesteht eine Funktion f (x) aus mehreren Summanden, so werden diese als einzelne Funktionen betrachtet und können auch einzeln aufgeleitet werden.
Ausführliche InfosBefindet sich ein Faktor vor der Potenz, der unabhängig von der Variablen x ist, kann dieser aus dem Integral gezogen
Ausführliche InfosMit der Potenzregel kann man für alle Funktionen der Form f (x) = xn direkt die Aufleitung angeben. Der Exponent n ist hierbei eine
Ausführliche InfosWir sind im vorherigen Artikel schon mit unbestimmten Integralen in Berührung gekommen. Das Ergebnis eines Integrals lässt sich als Fläche
Ausführliche InfosBei der Differentialrechnung haben wir bereits gelernt, wie man Funktionen ableitet. Was aber, wenn wir nur die Ableitung einer Funktion
Ausführliche InfosUm eine Fläche unter einer Kurve zu berechnen, nehmen Mathematiker unendlich viele kleine Rechtecke heran. Ihre Höhe entspricht der der y-Koordinate und die Breite ist möglichst klein bis gegen Null. Die Fläche jedes einzelnen Rechteckes zusammen ergibt die exakte Fläche des Integrals. Die Fläche eines Rechtecks errechnet sich aus der Höhe mal der Breite.
Wählt der Nutzer die Breite merkbar groß, entsteht eine Ungenauigkeit, weil jedes Rechteck am Eck entweder über oder unter die Linie heraus- oder herunterragt. Alle Rechtecke zusammen ergeben eine bestimmte Fläche. Fehlt ein Stück, befindet sich das zweite Eck rechts unter der Linie, spricht die Mathematik von der Untersumme. Um die Obersumme zu erhalten, wählt der Schüler das jeweils rechte Eck eines Rechteckes auf der Linie des Graphen. Allerdings entsteht auf diese Weise eine größere Summe als die eigentliche Fläche groß ist.
Ist an dieser Stelle die exakte Fläche verlangt, liegt die wirkliche Lösung zwischen der Ober- und Untersumme. Um die Ungenauigkeiten zu eliminieren wählt der Mathematiker eine unendlich kleine Breite, die gegen Null geht, für die Rechtecke aus. Unendlich viele kleine Rechtecke ergibt die Integralrechnung zur Berechnung einer Fläche.
Wer eine Fläche unter einer Funktion berechnen möchte, benötigt für diesen Schritt die Stammfunktion. Diese erhält der Mathematiker mithilfe der Integralrechnung. Allgemein ausgedrückt ist die Rechnung für das Integral nichts Anderes als die umgekehrte Differenzialrechnung. Die Stammfunktion bezeichnet die Aufleitung einer gegebenen Funktion. Leitet der Nutzer die Stammfunktion mit der Differenzialrechnung ab, erhält er wieder die Ausgangsfunktion.
Als Beispiel ist die Funktion f(x) = 4x gegeben. Führt der Mathematiker das Integral durch, erhält er die Funktion:
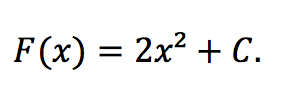
„C“ entspricht einer unbestimmten Konstante als Variable für alle verloren gegangenen Zahlen durch die Ableitung.
Die allgemeine Stammfunktion besitzt keine Grenzen, die Fläche zwischen der Kurve und der x-Achse ist unbestimmt. Der Bereich der Fläche grenzt sich in erster Linie durch den Funktionsgraphen nach oben und durch die x-Achse nach unten ein. Frei und noch zu bestimmen sind die Abgrenzungen auf der x-Achse und wie breit die Fläche des Integrals tatsächlich ist.
Diese Punkte auf der x-Achse benennt die Mathematik als untere und obere Integrationsgrenzen oder als Intervall bezeichnet. In diesem Schritt ist die Integralrechnung zweifach aufzulösen, einmal für den unteren und einmal für den oberen Wert. Die Differenz dieser Flächen ist die gesuchte Fläche des bestimmten Integrals.
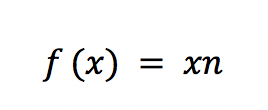
beschreibt eine Funktion mit einem Exponenten n. Diese Variable steht für eine beliebige rationale Zahl, was zur Erklärung der Potenzregel hilfreich ist. Integriert ein Mathematiker einen Term mit einem Exponenten, folgt daraus diese Regel:
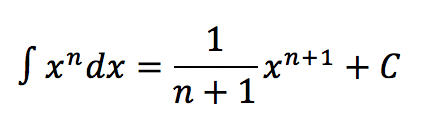
Zur Verdeutlichung ein kurzes Beispiel: Das Integral von:
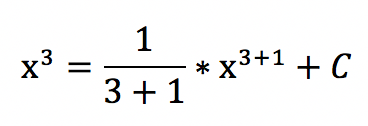
Die Faktorregel vereinfacht das Rechnen eines Integrales um einiges. Steht ein Faktor vor dem ![]() ist es erlaubt, das a herauszuheben und vor das Integralzeichen zu setzen. Der Faktor ist somit nicht Bestandteil der eigentlichen Integralrechnung.
ist es erlaubt, das a herauszuheben und vor das Integralzeichen zu setzen. Der Faktor ist somit nicht Bestandteil der eigentlichen Integralrechnung.
Weitere Rechenregeln des Integrals
Eine weitere essenzielle Regel bei der Anwendung einer Integration ist die sogenannte Summenregel. Besteht eine Funktion f(x aus mehreren Summanden g(x) + h(x) + … ist es möglich, alle Gleichungen gesondert zu betrachten. Aus diesem Anlass ergibt sich, dass aus dem Integral
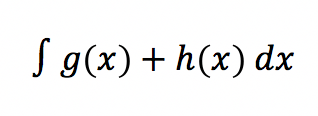
die einzelnen Integrale
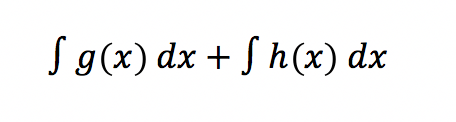
entstehen.
Nach demselben Prinzip funktioniert die Differenzregel. Der einzige Unterschied liegt darin, dass sich die beiden Terme nicht addieren, sondern subtrahieren. Dies vereinfacht weiteres die Berechnung der Stammfunktion.
Mit zunehmendem Theoriewissen, werden die Beispiele einer Integralrechnung komplexer. Für diesen Zweck um wieder Ordnung und Struktur einzubringen, entwickelten Mathematiker die partielle Integration. Sie kommt zur Anwendung, wenn bei einer Integralrechnung ein Produkt enthalten ist, welches ebenfalls von x abhängig ist.
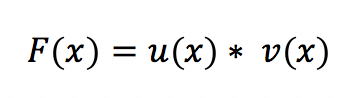
Um dieses Problem zu lösen, wählt der Anwender einen Term aus und bestimmt diesen zur Ableitung. Mit etwas Geschick entsteht dieser folgende Ausdruck:
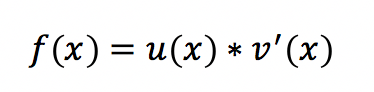
Die partielle Integration erfolgt ab dieser Stelle wie folgt:
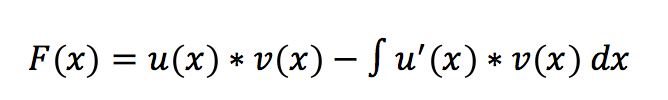
Für mehr Beispiele und einen tieferen Einblick genügt ein Klick im Inhaltsverzeichnis.
Die Substitutionsregel dient als Gegenelement der Kettenregel bei der Differentialrechnung. Die Regel an sich erscheint als schwer zu verstehen, allerdings ist der Umgang notwendig, um bei bestimmten Rechnungen schnell und einfach zur Lösung zu kommen.
Meist ist eine Integration nach x gefragt, obwohl weitere Variablen oder Terme, wie schwierige Winkelfunktionen vorkommen. Anstelle diese aufzulösen und lang und breit auszurechnen, ist es möglich, die Variablen als Zahlen anzusehen. Um diese Regel anzuwenden, ist es notwendig, die Schritte anhand eines Beispiels zu erklären. Dieses ist unter dem Link „Substitution“ im Inhaltsverzeichnis zu finden.
Verschiedene Aufgaben erfordern, dass die Fläche zwischen einem Graphen und der x-Achse zu berechnen sind. Was passiert, wenn die Kurve vom positiven in den negativen Bereich wechselt? In diesem Fall ist es notwendig, die bestimmte Integration am Nullpunkt zu unterteilen und zwei Integrationen durchzuführen.
Weil Flächen nicht negativ sein können, ist es erforderlich den Betrag der negativen Lösung zu nehmen, wodurch der Wert für sich positiv wird. Anschließend addiert der Mathematiker beide Flächen und erhält eine positive Gesamtfläche im bestimmten Intervall.
Ein weiterer Sonderfall ereignet sich, wenn die Fläche zwischen zwei Funktionen gefragt ist. In diesem Fall sind die Grenzen die Schnittpunkte beider Graphen. Die Fläche, die sich dazwischen erstreckt, gilt es zu berechnen. Für diesen Zweck ergibt sich folgende Formel:
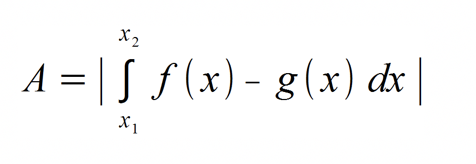
Der letzte Punkt des Inhaltsverzeichnisses ist eine tabellarische Übersicht. Sie dient als Vergleich zwischen der Differential- und Integralrechnung. Auf einem Blick findet der Nutzer wie sich der entsprechende Term in der Berechnung verhält. Diese kleine Formelsammlung vereinfacht das Anwenden und Erlernen des Integrals.
Das Thema ist umfassend und benötigt einiges an Grundwissen. Es verwirklicht neben der Differentialgleichung das zweite größte Themengebiet der fundamentalen Mathematik. Mit den weiterführenden Links im Inhaltsverzeichnis, ist eine schnelle Lösung in den einzelnen Bereichen möglich, sodass das Lernen mit Erfolg gelingt.