Was ist die E-Funktion?
Die Exponentialfunktion rein mathematisch
- Die Exponentialfunktion ist eine Berechnung nach dem Muster f(x) = ax
- A muss dabei größer als null sein und darf auch nicht den Wert 1 haben. Für y ist jeder Wert, abgesehen von plus und minus, unendlich möglich.
- Der Graph dieser Funktion hat bei dem Wert x = 0 stets den Wert 1. Dieser Wert ist vom Wert a unabhängig.
- Ist die Basis a größer als 1, liegt eine Wachstumsfunktion vor. Der Graph steigt zunächst langsam und dann immer schneller. Auch wenn die Zeichnung schon eine senkrechte Linie zu sein scheint, kann ein noch schnelleres Wachstum für größere x-Werte dargestellt werden.
- Ist die Basis kleiner als 1, ist die Funktion ein Verfallsprozess. Der Wert sinkt zunächst schnell, dann immer langsamer. Doch egal wie groß der Wert x eingesetzt wird, erreicht die Funktion doch nie den Wert null.
Diese Exponentialfunktionen haben eine große Bedeutung für die Beschreibung von Prozessen , bei denen das Ergebnis der Veränderung , also die Abnahme oder die Zunahme einer Größe die weitere Veränderung selbst wieder beeinflußt .
Dies kann man an folgenden Beispielen erklären :
Der radioaktive Zerfall .
Hierfür gilt : N = N tiefgestellt 0 mal e hoch minus Lamda (λ) t .
►N bezeichnet dabei die Anzahl der zum Zeitpunkt t noch nicht zerfallenen Atome einer radioaktiven Substanz .
►N tiefgestellt 0 bezieht sich auf die Anzahl der zum Zeitpunkt t = 0 vorhandenen , nicht zerfallenen Atome .
►Lambda gibt die für die Substanz charakteristische Zerfallskonstante an und
►T tiefgestellt H bezeichnet die Halbwertszeit .
►Die Halbwertszeit ist die Zeitspanne , innerhalb derer die Hälfte aller Atome zerfallen ist . Sie ist für die ►Substanz ebenfalls charakteristisch .
►Dabei gilt : Lambda mal T tiefgestellt H = ln 2
Grafik einer E-Funktion (Beispiel)
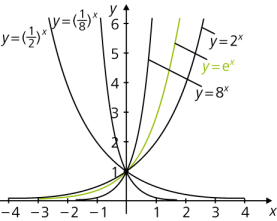
Bei e-Funktionen ohne einen Bruch oder eine Summe wie z.B. f(x)=x2⋅ek⋅x3 gibt es nur waagerechte Asymptoten.
- Extrempunkte und Wendepunkte gibt es nur, wenn die e-Funktion mit einer ganzrationalen Funktion verknüpft ist bzw. im Exponent eine ganzrationale Funktion steht, die mindestens Grad 2 besitzt
- Der Definitionsbereich einer e-Funktion ohne Bruch sind immer alle reellen Zahlen also D=IR.
- Ganz einfache e-Funktionen der Form f(x)=k∗eganzrationaleFunktion sind nur achsensymmetrisch, wenn im Exponent eine achsensymmetrische Funktion steht
- z.B. f(x)=2⋅e−3x4−x2.
- Punktsymmetrisch können einfache e-Funktionen nicht sein.
- e-Funktionen der Form f(x)= ganzrationale Funktion 1⋅eganzrationaleFunktion2 sind achsensymmetrisch, wenn beide ganzrationale Funktionen achsensymmetrisch sind
- z.B. f(x)=x2⋅e−3x2−2.
- e-Funktionen der Form f(x)= ganzrationale Funktion 1⋅eganzrationaleFunktion2 sind punktsymmetrisch, wenn die ganzrationale Funktion im Exponent achsensymmetrisch und die ganzrationale Funktion 1 punktsymmetrisch ist.
z.B. f(x)=x3⋅e−3x4+3.
Kurze Zusammenfassung
►Definition: Neben der definierenden Eigenschaft der Exponentialfunktion -f(x+y)=f(x)⋅f(y)f(x+y)=f(x)⋅f(y)- erfüllt die ee-Funktion folgende Gleichung:
f′(x)=f(x) f′(x)= f(x)
Diese Eigenschaft macht sie einzigartig.
►Wieso gilt diese Gleichung für ee?
Es ist bekannt, dass die Ableitung einer Exponentialfunktion f(x)=axf(x)=ax gegeben ist durch
f′(x)=ln(a)⋅axf′(x)=ln(a)⋅ax. Für die natürliche Exponentialfunktion mit Basis ee gilt also:
f′(x)=(ex)′=ln(e)⋅ex=ex=f(x)f′(x)=(ex)′=ln(e)⋅ex=ex=f(x)
Dabei wurde verwendet, dass der natürliche Logarithmus die Umkehrfunktion der natürlichen Exponentialfunktion ist und deswegen ln(e)=ln(e1)=1ln(e)=ln(e1)=1 gilt.
