Logarithmus
Der Logarithmus ist eine Verhältniszahl mit der man eine andere Zahl potenzieren kann, um eine bekannten Zahlenwert zu erhalten.
Den Logarithmus braucht man um Exponentialgleichungen y = ax zu lösen.
Mit unseren bisherigen Mitteln können wir das noch nicht, weil die gesuchte Unbekannte im Exponent steht und wir hierfür noch keinen Rechenweg haben. Der Logarithmus setzt genau in diese Lücke ein und hilft die Gleichung zu lösen.
Beispiel 1:
100 = 10x
Hier ist die Frage: „Wie oft muss ich 10 mit sich selbst multiplizieren, dass ich zu dem Ergebnis 10 komme?“
Diese Aufgabe können einige vielleicht bereits im Kopf rechnen oder wissen das Ergebnis für x durch vergangene Aufgaben.
Die Antwort: x=2, denn: 102 = 10 * 10 = 100.
Beispiel 2:
243 = 3x
Diese Aufgabe ist um einiges schwieriger. Daher brauchen wir nun die Logartihmusrechnung um unsere Gleichung lösen zu können.
Diese lautet:
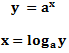
Man spricht: Der Logarithmus von y zur Basis a.
Wir müssen in diesem Fall den Logarithmus (abgekürzt log) zur Basis 3 von 243 nehmen. Als Ergebnis erhalten wir x. Wir haben beim Logarithmus also eine Basis und einen Wert von dem wir den Logarithmus nehmen.
Anwendung:
243 = 3x
x = log3(243)
x = 5
Probe:
35 = 3*3*3*3*3 = 405
Beispiel 3:
256 = 4x
Anwendung:
256 = 4x
x = log4(256)
x = 4
Probe:
44 = 4 * 4 * 4 * 4 = 256
Häufig benutzte Logarithmen
Es gibt einige Logarithmen die besonders häufig vorkommen. Dazu gehören auf jeden Fall der natürliche Logarithmus zur Basis e und der Zehnerlogarithmus zur Basis 10. Wir stellen diese beiden kurz vor.
Natürlicher Logarithmus
Der natürliche Logarithmus ![]() wird mit ln (logarithmus naturalis) abgekürzt. Er kommt besonders häufig bei Exponentialfunktionen vor.
wird mit ln (logarithmus naturalis) abgekürzt. Er kommt besonders häufig bei Exponentialfunktionen vor.
Eine normale Exponentialfunktion hat also die Form
![]()
e steht für die eulersche Zahl und ist gleich 2.71828…. e ist genau wie π eine irrationale Zahl.
Wenn wir nun folgende Gleichung lösen müssen:
![]()
benötigen wir den natürlichen Logarithmus (ln). Das ergibt:
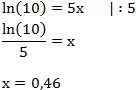
Wir machen noch einmal die Probe:
![]()
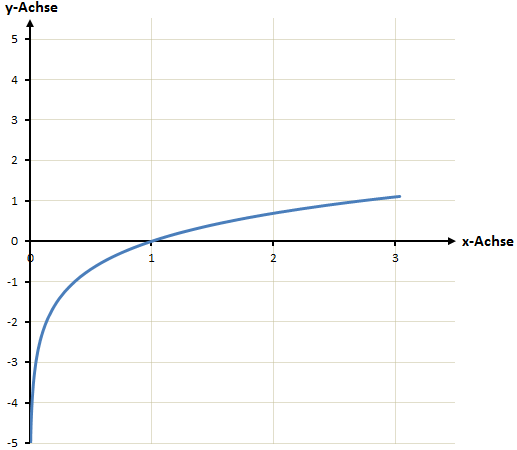
Der natürliche Logarithmus sieht so aus:
![]()
Zehnerlogarithmus
Der Zehnerlogarithmus ![]() wird mit lg abgekürzt. Teilweise findet man auch nur die Schreibweise „log“ für den Zehnerlogarithmus. Diese ist allerdings etwas widersprüchlich und sollte vermieden werden.
wird mit lg abgekürzt. Teilweise findet man auch nur die Schreibweise „log“ für den Zehnerlogarithmus. Diese ist allerdings etwas widersprüchlich und sollte vermieden werden.
Eine Exponentialfunktion mit der Basis 10 sieht so aus:
![]()
Wir lösen eine beispielhafte Exponentialfunktion:
![]()
Da diese Exponentialfunktion die Basis 10 hat, benötigen wir den Zehnerlogarithmus. Wir können die Gleichung also folgendermaßen umformen:
![]()
Das Ergebnis ist dann:
![]()
