Potenzfunktionen

Unter Potenzfuntionen versteht man elemantare mathematische Funktionen, die folgende Form haben:

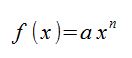
mathematische Funktion

Der Verlauf des Graphen hängt von der Potenz ab und ist einzuordnen in verschiedene Kategorien

n ist eine positive ganze gerade Zahl

Der Graph verläuft als achsensymmetrische Parabel. Darunter findet sich auch die Normalparabel f(x) = x². Davon zu unterscheiden sind die Parabeln 4. Grades, 6. Grades etc.

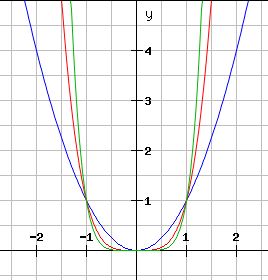
Normalparabel

blau: f(x) = x²
rot: f(x) = x⁴
grun: f(x) = x⁶

n ist eine positive ganze ungerade Zahl

Graphen mit diesen Potenzen verlaufen punktsymmetrisch zum Ursprung. Die Funktion f(x) = x³ nennt man auch kubische Funktion.

kubische Funktion

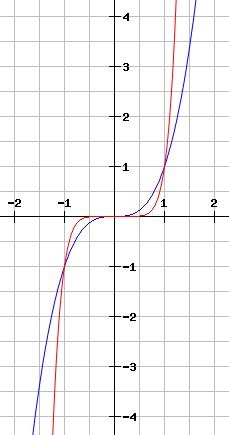
blau: f(x) = x³
rot: f(x) = x⁷

n ist eine negative ganze gerade Zahl

Diese Graphen heißen Hyperbel und sind achsensymmetrisch. Die Hyperbel nähert sich den Achsen an, erreicht sie aber nicht, dies nennt man asymptotisches Verhalten. z. B. x^-2, x^-4…

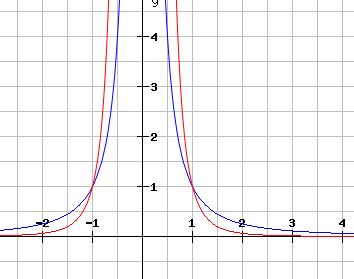
asymptotisches Verhalten

blau: f(x) = x^-2
rot: f(x) = x^-4

n ist eine negative ganze ungerade Zahl

Auch dieser Graphen werden Hyperbel genannt und auch verhalten sich asymptotisch. Wie auch die postiven ganzen ungeraden Potenzen sind sie punktsymmetrisch.

punktsymmetrisch

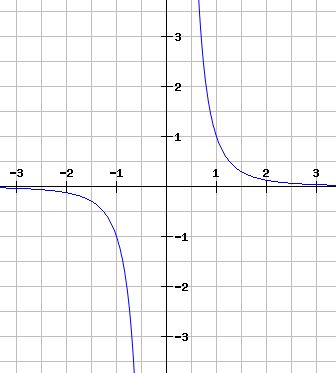
blau: f(x) = x^-3

Unser Lernvideo zu : Potenzfunktionen

Weitere Fälle

n ist gleich 1

Der Graph ist eine Gerade durch den Ursprung mit der Steigung a

a ist größer null und kleiner 1

Der Graph steigt flacher als der Normalgraph

a ist größer als 1

Der Graph steigt steiler als der Normalgraph

Interessante Fragen und Antworten zu Potenzfunktionen

Was passiert wenn man den Graphen einer Potenzfunktion verschiebt?

Gegeben sei die Funktionsgleichung einer Potenzfunktion:f(x)=a·x^n

a ist Element der reelen Zahlen, n ist Element der natürlichen Zahlen. Angenommen, dieser Funktionsgleichung wird ein Summand hinzugefügt. Es ergibt sich folgende Gleichung:

f(x)-> f(x)+c

In diesem Fall verschiebt sich der Graph der Funktion entlang der y-Achse nach oben und zwar exakt um den Wert c.

Wird der Summand abgezogen, ergibt sich folgende Funktionsgleichung:

f(x)-> f(x)-c

Hier verschiebt sich der Graph erneut entlang der y-Achse, allerdings nun in negative Richtung nach unten. Wird ein Summand c einer Funktion hinzugefügt oder abgezogen, entsteht hierdurch eine neue Funktion g(x). Diese gleicht dem Graphen der ursprünglichen Funktion f(x), ist jedoch um den Summanden c nach oben, beziehungsweise unten verschoben.

Es wird erneut die Funktionsgleichung f(x)=a·x^n betrachtet. Dieses Mal wird dem Argument x ein Summand c hinzugefügt.

a·x^n -> a·(x+c)^n

Nun verschiebt sich der Graph der Funktion entlang der x-Achse nach links und zwar erneut um den Summanden c. Wird c abgezogen, ergibt sich folgende Funktion:

a·x^n -> a·(x-c)^n

In diesem Fall verschiebt sich der Graph nicht entlang der x-, sondern entlang der y-Achse um den Summanden c.

Wie bestimmt man den Wertebereich einer Potenzfunktion?

Der Wertebereich einer Potenzfunktion wird auch Wertemenge bezeichnet. Soll man den Wertebereich einer Funktion bestimmen, hat man in der Regel eine Funktion gegeben, so wie den zu definierenden Bereich, den sogenannten „Definitionsbereich“. Der Wertebereich einer Potenzfunktion jedoch ist abhängig von a und n so wie dem Globalverhalten.Der gegebene Definitionsbereich legt fest, welche Werte in die angegebene Funktion eingesetzt werden dürfen. Um nun den Wertebereich einer Potenzfunktion zu bestimmen, sind die Werte des Definitionsbereiches für x in die Funktion einzusetzen. Da x die einzig Unbekannte Variabel in der Funktion ist, lässt sich diese nun einfach ausrechnen, so dass am Ende ein Ergebnis, y, und somit der Wertebereich der Potenzfunktion bestimmt ist.

Wie bestimmt man die Ableitung einer Potenzfunktion mit ganzzahligem Exponenten?

Von einer Funktion f(x) lautet die erste Ableitung f'(x). Mit Ihr kann man die Steigung der Funktion f(x) an einer beliebigen Stelle berechnen. Wenn wir eine Funktion mit ganzzahligem Exponenten haben, dann bestimmen wir daraus die erste Ableitung, indem wir den Exponenten um 1 reduzieren und den ursprünglichen Exponenten gleichzeitig als Multiplikator vor das x stellen.Wenn man das Zeichen „^“ als „hoch“ versteht, dann lautet es formal so:
f(x)=x^n -> f'(x)=n[x^(n-1)]

Beispiel 1: f(x)=x³ -> f'(x)=3x²
Beispiel 2: f(x)=2x³ -> f'(x)=6x²
Beispiel 3: f(x)=2x³+5 -> f'(x)=6x²+5

Wie bestimmt man die Nullstellen einer Potenzfunktion wenn der Exponent n = 2 oder n = 2 ist?

Diese Anleitung wird Ihnen helfen die Nullstellen einer Potenzfunktion zu ermitteln wenn der Exponent n= 2 beträgt.
Zunächst müssen Sie beachten, dass es sich bei der Funktion um eine quadratische Potenzfunktion handelt. Dies erkennen Sie daran, dass der Exponent n= 2 ist.
Die quadratische Potenzfunktion lautet f(x) = ax² + px + q. Da Sie die Nullstellen berechnen möchten, setzen Sie für f(x) die Zahl 0 ein und erhalten ax² + px + q = 0.
Im nächsten Schritt können Sie die pq-Formel anwenden. Diese kann jedoch nur angewendet werden, wenn der Koeffizient a = 1 ist und damit die Normalform vorliegt. Falls diese nicht gegeben ist, müssen Sie die Gleichung vorher durch den Faktor a teilen.
Die pq-Formel lautet x(1,2) = -(p/2) + – Wurzel aus [(p/2)²-q].
Berechnen Sie zuerst x(1) mit der Formel -(p/2) + Wurzel aus [(p/2)²-q].
Als zweites ermitteln Sie x(2) mit der Formel -(p/2) – Wurzel aus [(p/2)²-q] und erhalten als Lösungen Ihre beide Nullstellen.

Wie bestimmt man die Symmetrieeigenschaft einer Potenzfunktion?

Die Symmetrieeigenschaften einer Potenzfunktion lassen sich auch von Hand berechnen, obwohl die Nutzung eines geeigneten Tools viele Vorteile mit sich bringt. Die Potenzfunktion kann grundsätzlich achsen- oder punktsymmetrisch sein oder gar keine Symmetrie aufweisen.Um zu prüfen, ob die Potenzfunktion symmetrisch zur Y-Achse ist, wird x durch -x ersetzt. Wenn sich dadurch das Ergebnis nicht ändert, ist die Symmetrie gegeben. Mathematisch ausgedrückt bedeutet das: f (-x) = f (x). achsensymmetrische Potenzfunktionen bleiben bei diesem Austausch von x durch -x gleich, da sie auf beiden Seiten der Y-Achse identisch verlaufen.

Wenn die Potenzfunktion hingegen punktsymmetrisch zum Ursprung ist, gilt: f (-x) = -f (x). Auch dabei wird die Variable x in der Funktion durch -x ersetzt.

Für die Prüfung auf Achsen- und Punktsymmetrie ist dementsprechend nur eine Rechnung erforderlich. Das Ergebnis der Berechnung gibt anschließend Aufschluss darüber, welche Symmetrieeigenschaften die Potenzfunktion aufweist.

Wie kann man den Graphen einer Potenzfunktion zeichen, wenn nur die Funktionsgleichung gegeben ist?

Der Verlauf des Graphen einer Potenzfunktion ergibt sich aus dem Aufbau der Potenzfunktion.Sehen wir uns den Aufbau einer Potenzfunktion einmal an:

F (x) = a mal X hoch n

Hieraus ergeben sich 4 Fälle.

1. Fall
n ist gerade und positiv.
Diese Information sagt uns, dass es sich hier um eine Parabel handelt.
Nun entscheidet das Vorzeichen von a wie die Parabel verläuft.
Ist a positiv, so handelt es sich um eine Parabel, deren Tiefpunkt die 0 ist.
Ist a negativ, so handelt es sich um eine Parabel, deren höchster Punkt die 0 ist.

2. Fall

n ist gerade und positiv.

In diesem Falle handelt es sich um eine Gerade. Der Verlauf dieser Gerade wird durch das Vorzeichen von a bestimmt.
Ist a positiv, so steigt die Gerade in ihrem Verlauf nach rechts an.
Ist a negativ, so fällt die Gerade nach rechts ab.

3. Fall
N ist negativ und gerade.
In diesem Falle ist der Graph eine Hyperbel. Auch hier wird ihr Verlauf vom Vorzeichen der Variable a bestimmt.
Ist a negativ, befinden sich die Äste der Hyperbel unterhalb der X-Achse, ist a positiv, befinden sie sich oberhalb der X-Achse.

4. Fall
N ist negativ und ungerade.
Auch hier bildet der Graph eine Hyperbel. Die Variable A bestimmt auch hier, wo sich die Äste der Hyperbel befinden.
Ist a positiv, dann befinden sie sich im 1. Und im 3. Quadranten, ist a negativ, dann befinden sie sich im 2 und 4 Quadranten.

Wie prüft man nach ob eine gegebene Wertetabelle einer Potenzfunktion gehört?

Gegeben sind die Wertetabelle eine Funktion, also mehrere Zahlenpaare x und y sowie die Funktionsgleichung f(x) = ax n.
Durch Einsetzen der ersten beiden Zahlenpaare aus der Wertetabelle in die Funktion ermittelt man durch diverse Umformungen die Parameter a und n und erhält somit konkrete Werte für diese Parameter. Somit hat man dann die Funktion gefunden, die die ersten beiden Zahlenpaare enthält.
Dann setzt man für x die übrigen Zahlen aus der Wertetabelle in die Funktionsgleichung ein und überprüft, ob das Ergebnis dem jeweiligen y-Wert aus der Wertetabelle entspricht. Ist dies der Fall, so liegt eine Potenzfunktion vor, im anderen Fall nicht.