Polstellen
Eine Polstelle – auch nur als Pol bezeichnet – ist eine nicht hebbare Definitionslücke, in deren Umgebung die Funktionswerte gegen (minus) unendlich laufen.
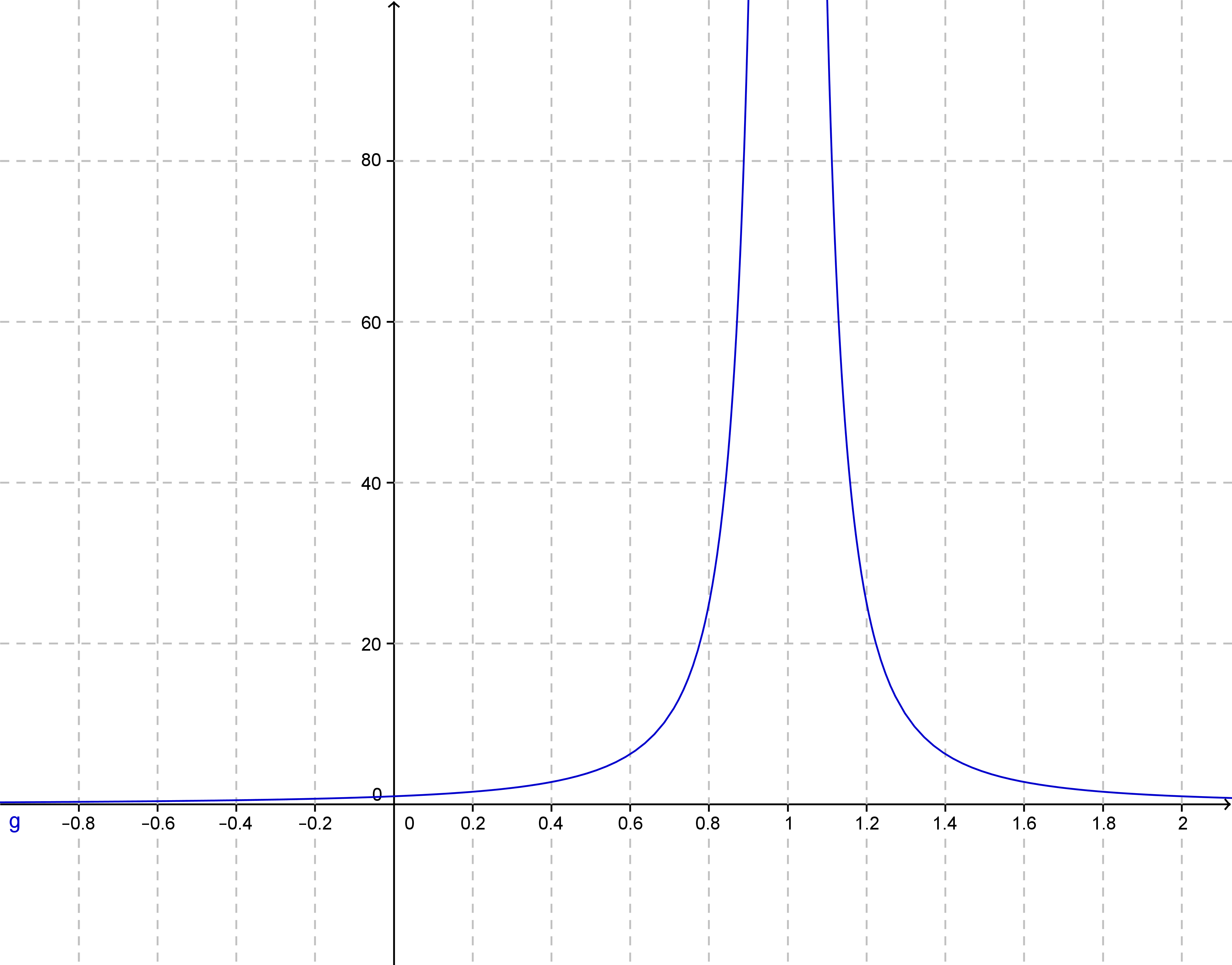
Beim vorliegenden Graph ist eine Polstelle bei x = 1 zu erkennen. Vor und nach der Polstelle nähert sich der Graph einer imaginären Geraden an, die parallel zur y-Achse ist. Solche Polstellen sind häufig bei gebrochenrationalen Funktionen zu beobachten.
Unser Lernvideo zu : Polstellen
Um eine gebrochenrationale Funktion auf Polstellen zu untersuchen, wird zunächst der Nenner auf Nullstellen geprüft. Liegen dort welche vor, ist zusätzlich zu ermitteln, ob diese auch Nullstellen des Zählers sind. Ist die Nullstelle des Nenners nicht auch eine Nullstelle des Zählers, so liegt eine Polstelle vor.
Beispiel 1
1. Schritt
Nenner auf Nullstellen prüfen
| x – 2 | = | 0 | | +2 |
| x | = | 2 |
2. Schritt
x-Wert in Zähler einsetzen
Da der Zähler hier unabhängig von x ist, entfällt dieser Schritt.
→ Es liegt eine Polstelle bei x = 2 vor.
Beispiel 2
1. Schritt
Nenner auf Nullstellen prüfen
| (x + 1)2 | = | 0 | | √ | |
| x + 1 | = | 0 | | -1 | |
| x | = | -1 |
2. Schritt
x-Wert in Zähler einsetzen
x + 1 = (-1) + 1 = 0
Da für den selben x-Wert auch im Zähler eine Nullstelle vorliegt, ist zu prüfen, ob die Definitionslücke hebbar ist. Wir faktorisieren hierfür unseren Term.
Setzen wir nun x = -1 ein, wird der Nenner gleich Null ohne dass der Zähler ebenfalls eine Nullstelle aufweist. Es handelt sich somit nicht um eine hebbare Definitionslücke, sondern eine Polstelle.
