Wendepunkte
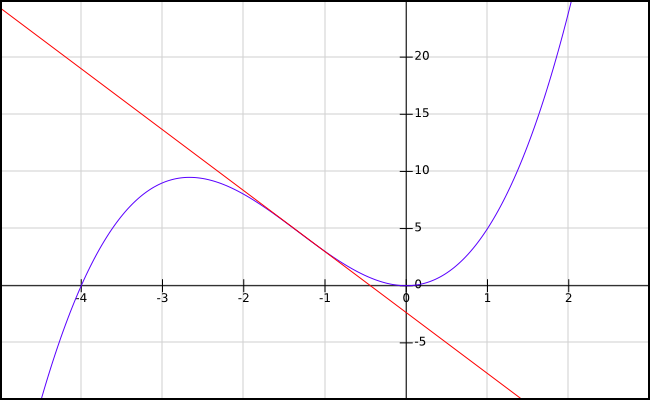
Der Wendepunkt eines Funktionsgraphen ist der Punkt, an dem der Graph sein Krümmungsverhalten ändert. Entweder wechselt er von einer Links- in eine Rechtskurve oder wie in unserem Beispiel von einer Rechts- in eine Linkskurve. Der blaue Graph stellt hier die Funktion f(x) = x3 + 4x2 mit einem Wendepunkt bei x = – 4/3 dar.
Die Krümmung wird durch die 2. Ableitung beschrieben. Wenn diese ihr Vorzeichen ändert, also gleich Null ist, liegt in der Stammfunktion ein Wendepunkt vor. Demnach lauten die Bedingungen für einen Wendepunkt wie folgt:
- Notwendige Bedingung: f “(x) = 0
- Hinreichende Bedingung: f “'(x) ≠ 0
→ wenn f “'(x) < 0, dann Links-rechts-Wendestelle
→ wenn f “'(x) > 0, dann Rechts-links-Wendestelle
Die rote Funktion in der Abbildung zeigt die sogenannte Wendetangente. Sie schneidet die Stammfunktion genau an ihrem Wendepunkt. Außerdem entspricht ihre Steigung genau der Steigung der Stammfunktion am Wendepunkt.
Wendepunkt berechnen
Um den oder die Wendepunkte zu bestimmen, hält man sich am besten an folgende Kochrezept:
- Stammfunktion dreimal ableiten
- Notwendige Bedingung prüfen, also 2. Ableitung gleich Null setzen
→ wenn kein x vorhanden, dann kein Wendepunkt - Hinreichende Bedindung prüfen, also alle erhaltenen x-Werte in 3. Ableitung einsetzen
→ wenn f “'(x)=0, dann kein Wendepunkt - x-Werte in Stammfunktion einsetzen, um dazugehörige y-Werte zu erhalten
Beispiel
f(x) = x3 – 6x2 + 5x
1. Schritt
Stammfunktion dreimal ableiten
f ‚(x) = 3x2 – 12x + 5
f “(x) = 6x – 12
f “'(x) = 6
2. Schritt
Notwendige Bedingung prüfen
| f “(x) = 0 | |
| 6x – 12 = 0 | | +1 |
| 6x = 12 | | :6 |
| x = 2 |
→ potenzieller Wendepunkt liegt vor
3. Schritt
Hinreichende Bedingung prüfen
(Hinweis: Hier ist die 3. Ableitung eine Konstante und ergibt für jeden x-Wert deshalb 6.)
f “'(2) = 6 ≠ 0
→ Wendepunkt liegt vor
optional:
f “'(2) = 6 > 0 , also Rechts-links-Wendestelle
4. Schritt
y-Wert bestimmen
y = f(2)
y = 23 – 6·22 + 5·2
y = -6
→ Demnach liegt für die Funktion ein Wendepunkt bei ( 2 | -6 ) vor.
Wendetangente berechnen
Ist der Wendepunkt einer Funktion bekannt, kann die dazugehörige Wendetangente bestimmt werden. Die Wendetangente ist eine Gerade, demnach hat sie die Form y = mx + b. Die Variable m ist die Steigung der Wendetangente und entspricht der Steigung der Stammfunktion am Wendepunkt. Dementsprechend erhalten wir m, indem wir den x-Wert des Wendepunkts in die 1. Ableitung einsetzen. Die Variable b ist der Schnittpunkt der Wendetangente mit der y-Achse und lässt sich mit Wissen um den Wendepunkt anschließend ebenfalls bestimmen.
Beispiel
g(x) = mx + b
1. Schritt
m bestimmen, also x-Wert des Wendepunkts in 1. Ableitung einsetzen
m = f ‚(2)
m = 3·22 – 12·2 + 5
m = -7
2. Schritt
b bestimmen
Der Wendepunkt ist ein bereits bekannter Punkt auf der gesuchten Wendetangente. Setzen wir dessen Werte für x und y und den errechneten Wert für m in die Geradengleichung ein, lässt sich diese nach b lösen.
y = mx + b
| -6 = -7·2 + b | |
| -6 = -14 + b | | +14 |
| 8 = b |
b = 8
3. Schritt
Wendetangente bilden
g(x) = mx + b
m = -7
b = 8
→ g(x) = -7x + 8
Sonderfall: Sattelpunkt
Ein Wendepunkt mit der Steigung Null heißt Sattelpunkt.
Beispiel
f(x) = x3 – 3x2 + 3x
1. Schritt
Stammfunktion dreimal ableiten
f ´(x) = 3x2 – 6x +3
f ´´(x) = 6x – 6
f ´´´(x) = 6
2. Schritt
Notwendige Bedingung prüfen
f “(x) = 0
6x – 6 = 0
x = 1
3. Schritt
Hinreichende Bedingung prüfen
f ´´´(1) = 6 ≠ 0
→ Wendepunkt liegt vor
4. Schritt
y-Wert bestimmen
f(1) = 13 – 3·12 + 3·1
f(1) = 1
→ Wendepunkt liegt bei ( 1 | 1 ) vor
5. Schritt
Wurden schon die Extremwerte bestimmt, sollte der Wert x = 1 bereits aufgefallen sein. An dieser Stelle ist zwar die notwendige Bedingung f ‚(x) = 0 für Extremwerte erfüllt, die hinreichende Bedingung f “(x) ≠ 0 jedoch nicht.
Falls direkt auf Wendepunkte geprüft wurde, sollte der x-Wert mit Hinblick auf potenzielle Stallelpunkte immer zusätzlich in die 1. Ableitung eingesetzt werden.
f ´(1) = 3·12 – 6·1 + 3
f ´(1) = 0
→ Somit erfüllt x = 1 die zusätzliche Bedingung f ´(x) = 0 und es liegt ein Sattelpunkt vor.
Zusammengefasst muss für einen Sattelpunkt also gelten:
- f ‚(x) = 0
- f “(x) = 0
- f “'(x) ≠ 0
