Symmetrieverhalten

Das Symmetrieverhalten beschreibt, ob eine zu untersuchende Funktion symmetrisch zu einer Achse (in der Regel die y-Achse) oder einem Punkt (in der Regel der Ursprung) ist. Im Folgenden sind beide Fälle dargestellt, wobei der linke Graph Achsensymmetrie zur y-Achse und der rechte Graph Punktsymmetrie zum Ursprung aufweist.

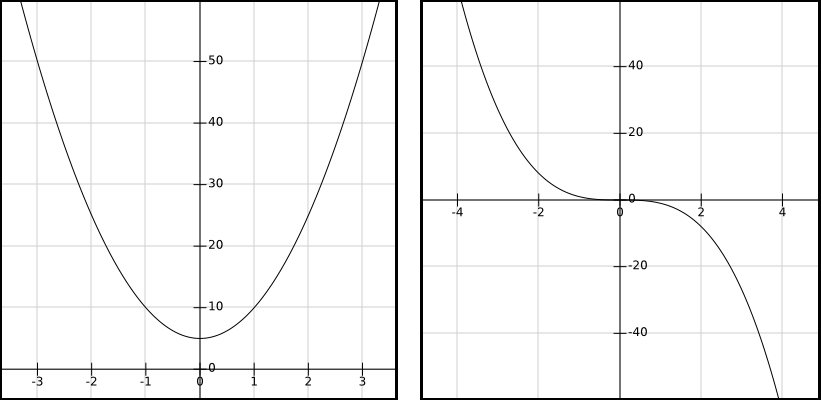
Dazu gelten folgende Bedingungen:

• Achsensymmetrie zur y-Achse liegt vor, wenn gilt f (x) = f (-x)
• Punktsymmetrie zum Ursprung liegt vor, wenn gilt f (x) = –f (-x)

Beispiel 1

f (x) = x³ + 2x

Schritt 1
Es ist sinnvoll, zunächst f(-x) zu bestimmen. Dafür setzen wir –x für alle x der Funktion ein, wobei besonders auf die Vorzeichen zu achten ist.

f(-x) = (-x)³ + 2⋅(-x)
f(-x) = –x³ – 2x

Schritt 2
Bedingung für Achsensymmetrie prüfen

• Bedingung: f(x) = f(-x)

In unserem Beispiel:
x³ + 2x ≠ –x³ – 2x
f(x) ≠ f(-x)

Daraus folgt, dass keine Achsensymmetrie vorhanden ist.

Schritt 3
Bedingung für Punktsymmetrie prüfen

• Bedingung: f(x) = –f(-x)

Um –f(-x) zu erhalten, multiplizieren wir f(-x) aus dem ersten Schritt mit (-1).
–f(-x) = f(-x) ⋅ (-1) = (-x³ – 2x) ⋅ (-1) = x³ + 2x

Nun vergleichen wir das Ergebnis mit f(x).
x³ + 2x = x³ + 2x
f(x) = –f(-x)

Daraus folgt, dass eine Punktsymmetrie zum Ursprung vorliegt.

Beispiel 2

f (x) = x³ + 2x² + 3

Schritt 1
Wir bestimmen wieder zunächst f(-x).

f(-x) = (-x)³ + 2⋅(-x)² + 3
f(-x) = –x³ + 2x² + 3

Schritt 2
Bedingung für Achsensymmetrie prüfen

• Bedingung: f(x) = f(-x)

In unserem Beispiel:
x³ + 2x² + 3 ≠ –x³ + 2x² + 3
f(x) ≠ f(-x)

Daraus folgt, dass keine Achsensymmetrie vorhanden ist.

Schritt 3:
Bedingung für Punktsymmetrie prüfen

• Bedingung: f(x) = –f(-x)

Dazu multiplizieren wir f(-x) aus dem ersten Schritt wieder mit (-1) und erhalten:
–f(-x) = f(-x) ⋅ (-1) = (-x³ + 2x² + 3) ⋅ (-1) = x³ – 2x² – 3

Wir überprüfen nun, ob die Bedingung erfüllt wird.
x³ + 2x² + 3 ≠ x³ – 2x² – 3
f(x) ≠ –f(-x)

Daraus folgt, dass keine Punktsymmetrie vorhanden ist.
Die Funktion ist damit weder achsen- noch punktsymmetrisch.

 

Beispiel 3

f (x) = 3x²

Schritt 1:
Wir bestimmen zunächst f(-x).

f(-x) = 3⋅(-x)²
f(-x) = 3x²

Schritt 2:
Bedingung für Achsensymmetrie prüfen

• Bedingung: f(x) = f(-x)

3x² = 3x²
f(x) = f(-x)

Daraus folgt, dass die Bedingung erfüllt ist und unsere Funktion achsensymmetrisch zur y-Achse ist.

Schritt 3:
Bedingung für Punktsymmetrie prüfen

Eine Funktion kann nicht achsen- und punktsymmetrisch sein, weshalb wir nicht weiter auf Punktsymmetrie untersuchen müssen.

 

• Allgemein kann man sagen, dass Funktionen mit ausschließlich geraden Exponenten ohne Absolutglied immer achsensymmetrisch sind und Funktionen mit ausschließlich ungeraden Exponenten ohne Absolutglied immer punktsymmetrisch sind.