Nullstellen (Grundlagen)

Im Rahmen der Kurvendiskussion ermittelt man die markanten Punkte einer Funktion, zu denen auch die Nullstellen gehören. Nullstellen sind die Schnittpunkte der Funktion mit der x-Achse des Koordinatensystems.

Welches Verfahren zur Bestimmung der Nullstellen bei welcher Funktion zum Einsatz kommt, ist abhängig vom Grad der Funktion. Im Folgenden werden die Verfahren für Funktionen ersten bis dritten Grades erläutert.

Funktion 1. Grades

Liegt eine Funktion ersten Grades vor, ist das Berechnen der Nullstellen noch recht simpel und bedarf nur zwei Schritte:

1. Funktion gleich Null setzen, also y = 0 bzw. f(x) = 0
2. Gleichung nach x auflösen

Beispiel

f(x) = 3x + 6

1. Schritt:
f(x) = 0
3x + 6 = 0
2. Schritt
3x + 6 = 0	| -6
3x = -6	| :3
x = -2

 

Funktion 2. Grades

Fall A

Liegt eine Funktion zweiten Grades vor, die in jedem Term ein x enthält, kann man dieses ausklammern, um die Gleichung daraufhin wie gewohnt zu lösen. Man geht also wie folgt vor:

1. Funktion gleich Null setzen
2. x ausklammern
3. Gleichung in Klammern nach x auflösen

Beispiel

f(x) = 2x² + 2x

1. Schritt
f(x) = 0
2x2 + 2x = 0
2. Schritt
x (2x + 2) = 0
x1 = 0
3. Schritt
2x + 2 = 0	| -2
2x = -2	| :2
x2 = -1

Somit erhalten wir für x zwei Lösungen. Zum einen sieht man im 2. Schritt, dass die Funktion – unabhängig vom Inhalt der Klammer – gleich Null wird, wenn x₁ = 0 ist. Außerdem ergibt die Funktion ebenfalls Null, wenn die Klammer gleich Null ist, weshalb wir deren Inhalt im 3. Schritt gleich Null setzen und nach x auflösen. Dadurch erhalten wir als zweite Lösung x₂ = -1

Fall B

Enthält die zu untersuchende Funktion zweiten Grades auch einen Term ohne die Variable x, kann die pq-Formel verwendet werden. Man geht wie folgt vor:

1. Funktion gleich Null setzen
2. x² freistellen, p und q ermitteln
3. p und q in Formel einsetzen

Beispiel

f(x) = 2x² + 8x – 10

1. Schritt
f(x) = 0
2x² + 8x -10 = 0
2. Schritt
2x² + 8x -10 = 0	| :2
x² + 4x -5 = 0
p = +4 und q = -5
3. Schritt

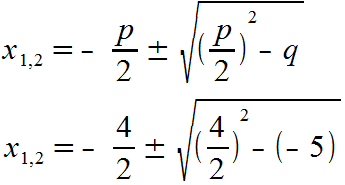
x₁ = -2 + 3 = 1    und    x₂ = -2 – 3 = -5

Funktion 3. Grades

Bei Funktionen dritten Grades, sogenannten Kubik-Funktionen, kann die Nullstelle mithilfe von Polynomdivision gelöst werden.

Beispiel

f(x) = 2x³ – 14x – 12

1. Schritt

Die erste Nullstelle findet man durch Raten, wobei es hierbei einen Trick gibt. Sie ist immer ein Teiler des Absolutgliedes, sowohl positiv als auch negativ. In unserem Beispiel ist die 12 das Absolutglied und durch ±1, ±2, ±3, ±4, ±6, ±12 teilbar. Jetzt wird probiert:

Einsetzen von +1:
2 ⋅ 1³ – 14 ⋅ 1 -12 = -24

Einsetzen von -2:
2 ⋅ (-2)³ – 14 ⋅ (-2) -12 = 0           → Treffer!

Durch Raten haben wir die erste Nullstelle bei x₁ = -2 gefunden.

2. Schritt:

Jetzt wird mit der ersten Nullstelle, in unserem Beispiel also -2, der Linearfaktor gebildet.  Da wir eine negative Zahl haben und beim Linearfaktor immer das Vorzeichen getauscht wird, müssen wir mit (x – x₁) = (x + 2) weiterarbeiten.

Aufgrund der Übersicht führen wir noch 0x² in die Funktion ein.

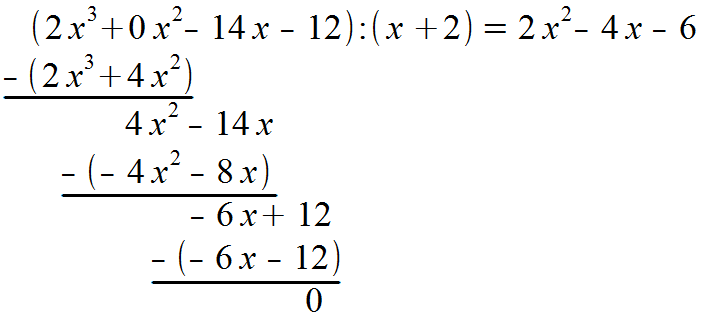
Durch eine Probe können wir herausfinden, ob wir richtig gerechnet haben.

Probe:

(2x³ – 4x – 6) ⋅ (x + 2) = 2x³ – 4x² – 6x +4x² – 8x – 12 = 2x³ – 14x – 12

Da wir unsere Ausgangsfunktion erhalten haben, wurde richtig gerechnet.

Das Ergebnis der Polynomdivision 2x² – 4x – 6 liefert uns mit Hilfe der pq-Formel (p = -2 und q = -3) zwei weitere Nullstellen bei x₂ = 3 und x₃ = -1.