Nullstellen (fortgeschritten)
Substitutionsverfahren
Liegt eine Funktion vierten Grades vor, bietet sich oft das Substitutionsverfahren an.
Beispiel
f(x) = x4 – 10x2 + 9
1. Schritt: Gleich Null setzen
f(x) = 0
x4 – 10x2 + 9 = 0
2. Schritt: Substitution
Wir können x2 = z substituieren und erhalten:
0 = x4 – 10x2 + 9 | z = x²
0 = z² – 10z + 9
Wir erhalten eine quadratische Gleichung, die mit Hilfe der pq-Formel zu lösen ist.
z1,2 =5 ± √16
z1 = 9
z2 = 1
3. Schritt: Rücksubstitution
Es ist jedoch nicht z, sondern x gesucht ist. Da x² = z ist, folgt durch Umformen x = ±√z und wir erhalten:
x1 = + √9 = 3
x2 = – √9 = – 3
x3 = + √1 = 1
x4 = – √1 = -1
Das Substitutionsverfahren findet immer dann Anwendung, wenn sich eine Funktion höheren Grades auf eine quadratische Funktion reduzieren lässt.
Näherungsverfahren
Falls keines der vorgestellten Verfahren anwendbar ist, können wir auf das Näherungsverfahren zurückgreifen. Dazu legen wir als erstes eine Wertetabelle an, um einen geeigneten Startwert zu finden.
Beispiel
f(x) = –x3 – 4x + 10
1. Schritt
Wir setzen für x die Werte von -4 bis 4 ein und erhalten folgende Ergebnisse.
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| y | 90 | 49 | 26 | 15 | 10 | 5 | -6 | -29 | -70 |
2. Schritt
Wir schauen uns die Stellen in der Wertetabelle an, zwischen denen ein Vorzeichenwechsel stattfindet. In unserem Beispiel geschieht das zwischen den Stellen x = 1 und x = 2. Hier muss der Graph also die x-Achse schneiden und somit eine Nullstelle vorliegen.
3. Schritt
Wir legen einen Startwert fest. Man kann hier jetzt 1 oder 2 als Startwert wählen. Grundsätzlich ist es immer sinnvoller den x-Wert zu nehmen, dessen y-Wert näher an Null liegt. Das ist in unserem Fall x = 1.
4. Schritt
Die Formel für das Newton-Verfahren lautet:
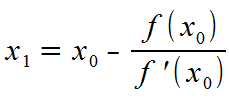
Unser x0 ist der Startwert 1. Nun ist noch die erste Ableitung der Funktion zu bilden.
f´(x) = -3x2 – 4
Eingesetzt in die Formel ergibt dies:
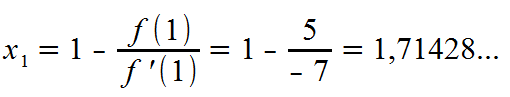
5. Schritt
Der Wert x = 1,71428 wird wieder in die Formel eingesetzt, das Ergebnis als neuer Startwert festgelegt und dies solange wiederholt, bis sich zwei Nachkommastellen nicht mehr ändern.
Wir erhalten:
x2 = 1,5676…
x3 = 1,5535…
x4 = 1,5567…
Ab x4 ändern sich ersten zwei Nachkommastellen nicht mehr und wir sind mit unserer Nullstellenbestimmung genau genug.
