Hypergeometrische Verteilung
Hypergeometrische Verteilung
Was ist die Hypergeometrische Verteilung?
- Die hypergeometrische Verteilung ist eine diskrete Wahrscheinlichkeitsverteilung in der Stochastik. Es wird von einer dichotomen Grundgesamtheit ausgegangen. Dieser Gesamtheit werden in einer Stichprobe zufällig Elemente nacheinander ohne Zurücklegen entnommen.
Kurzgefasst: Man kann sich die hypergeometrische Verteilung einfach als Urne vorstellen, bei der Kugeln ohne Zurücklegen entnommen werden.
Die mathematische Definition der Formel
- Sei N die Anzahl der Elemente in der Grundgesamtheit; M die Anzahl der Elemente, die für uns günstig sind; n sei die größe der Stichprobe (daher die Anzahl der Elemente, die wir „entnehmen“ wollen); k die Anzahl der Elemente aus M, die in n enthalten sind.
ist der Binomialkoeffizient.
Mathematische Definitionen zu verstehen fällt für viele schwer. Sicherlich fragt ihr euch, was die einzelnen Buchstaben bedeuten und wie man das ganze verständlich umsetzten kann. Hier eine kleine zusammenfassung der Formel

Unser Lernvideo zu : Hypergeometrische Verteilung
Nun berechnen wir gemeinsam einen Beispiel dazu:
Aufgabe:
- Es sind 14 Kugeln vorhanden, 5 rote, die die erfahrenen Personen repräsentieren, und 9 schwarze Kugeln, die die übrigen Kandidaten repräsentieren. Nun werden 5 Kugeln ohne Zurücklegen gezogen. Es ist von daher die Hypergeometrische Verteilung anzuwenden.
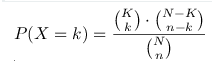
n = 5 (Es werden 5 Personen für das Komitee ausgewählt)
N = 14 (Es stehen 14 Personen zur Auswahl)
M = 5 (Anzahl der erfahrenen Personen)
Gesucht die Wahrscheinlichkeit x = 3
Nun setzen wir unsere Zahlen in die Formel ein:
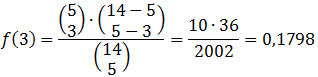
Die Wahrscheinlichkeit, dass genau drei erfahrene Personen in das Komitee gelost werden, beträgt 17,98%.

