Laplace Experiment
„Lasst uns eine Münze werfen.“ Hättet ihr vielleicht nicht gedacht, dass man die Wahrscheinlichkeit berechnen kann, ob im nächsten Moment Zahl oder Kopf erscheint? Dann solltet ihr unbedingt einen Blick auf das Laplace Experiment werfen.
Was ist die Laplace Regel
- Der französische Mathmatiker Pierre-Simon Laplace (1749 – 1827) machte Entdeckungen in der Wahrscheinlichkeitsrechnung, die in der modernen Mathematik heute unverzichtbar sind. Er hat herausgefunden, dass bei manchen Zufallsexperimenten alle Ergebnisse gleichwahrscheinlich sind. Bei einem Münzwurf ist es zum Beispiel gleichwahrscheinlich, auf welcher Seite die Münze landet – Kopf oder Zahl. Zufallsexperimente wie diese nennt man daher nach dem französischen Mathematiker Laplace-Zufallsexperimente
Laplace Wahrscheinlichkeit berechnen
Vorgehensweise
- Anzahl aller überhaupt möglichen Elementarereignisse berechnen
- Anzahl der Elementarereignisse berechnen, bei denen E eintritt
- Laplace-Wahrscheinlichkeit berechnen
Formel Laplace Experiment

Einführung in das Laplace Experiment
Natürlich gehen wir davon aus, dass in Wirklichkeit die Karten gezinkt und Münzen und Würfel manipuliert sein können. Dennoch brauchen wir für die Berechnung und den Versuch eine exaktere Form der Wirklichkeit.
Einen Laplace Versuch gibt es nur in der Theorie. Wir betrachten das Münzbeispiel.
Wenn Du eine reale Münze wirfst, kann sie auf die eine oder andere Seite fallen. Da aber eine Münze mechanisch hergestellt ist, kann sie Unregelmäßigkeiten aufweisen, die dazu führen, dass sie öfter auf die eine Seite fällt als auf die andere. Außerdem kann eine Münze auch in sehr seltenen Fällen auf der Kante stehenbleiben.
Laplace hat sich für seine Wahrscheinlichkeitsrechnung eine Münze vorgestellt, die wirklich genau zu 50% auf der einen oder anderen Seite zu liegen kommt. Außerdem fällt die Laplace Münze nie auf die Kante. Es handelt sich also um das theoretische Idealbild einer Münze.
Dementsprechend gibt es dann auch andere Lapalace-Zufallsgeräte (z.B. Würfel).
Wird ein Zufallsexperiment mit einer endlichen Ergebnismenge E hinreichend oft wiederholt und zeigt sich dabei, daß keines der Elementarereignisse gegenüber einem anderen bevorzugt auftritt, so werden alle Ereignisse stets näherungsweise gleich häufig auftreten und wir sprechen von einem Laplace-Experiment
Wann die Laplace-Formel nicht gilt
Beim Münz- und Würfelwurf funktioniert die Anwendung der Laplace-Formel prima. Bei vielen anderen Zufallsexperimenten allerdings nicht. Sie kann nur dann angewendet werden, wenn alle Elementarereignisse die selbe Eintrittswahrscheinlichkeit haben. Bei der Münze und beim Würfel ist das gegeben: Per Zufall erscheint eine der Seiten und keine hat eine höhere Wahrscheinlichkeit als irgendeine andere Seite. Bereits bei einem gezinkten Würfel, der z. B. in 50% aller Fälle eine 6 ergibt und in 50% aller Fälle eine Augenzahl zwischen 1 und 5 versagt die Laplace-Formel.
Wieso kann die Formel nun nicht auf solche Zufallsexperimente angewendet werden?
Das liegt daran, dass in der Formel nur die Anzahlen eine Rolle spielen: Die Anzahl aller gesuchten Elementarereignisse wird durch die Anzahl aller möglichen Elementarereignisse geteilt. Verwendet man nur die Anzahlswerte, dann setzt man voraus, dass die Eintrittswahrscheinlichkeit jedes einzelnen Elementarereignisses gleich ist — andernfalls müssten auch die Eintrittswahrscheinlichkeiten der Elementarereignisse in der Formel auftauchen.
⇒Die Laplace-Formel darf nur dann verwendet werden, wenn jedes Elementarereignis die selbe Eintrittswahrscheinlichkeit hat (siehe z. B. Würfel oder Münzwurf)
Bei den folgenden Experimenten und Ereignissen handelt es sich um das Laplace Experiment:
- Münze werfen
- Würfeln
- Karte ziehen
- Glücksrad drehen
- Gameshow Prinzip – Tür, Box oder Durchgang wählen
Laplace Experiment
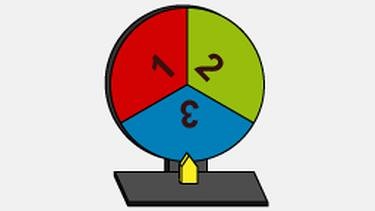
Beim Drehen des abgebildeten Glücksrades ergibt sich folgendeErgebnismenge:
Ω = {1, 2, 3}
Beim Drehen des Glücksrades kannst du als Ergebnis also entweder die 1, die 2 oder die 3 erhalten.
Da die Flächen der jeweiligen Zahlen gleich groß sind, besitzt jedes Ergebnis die gleiche Wahrscheinlichkeit beim Drehen angezeigt zu werden.
Kein Laplace Experiment
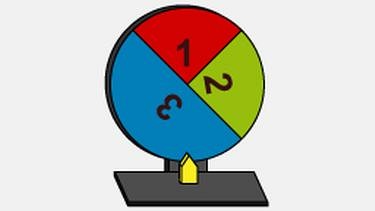
Auch bei diesem Glücksrad ergibt sich beim Drehen wieder die Ergebnismenge:
Ω = {1, 2, 3}.
Da die Fläche der Zahl 3 jedoch größer ist, als die Flächen der Zahlen 1 und 2, besitzen die drei Zahlen nicht mehr die gleiche Wahrscheinlichkeit. Die Wahrscheinlichkeit von Zahl 3 ist höher als die der Zahlen 1 und 2.
Beispiel
Wir werfen einen sechsseitigen Würfel und möchten verschiedene Wahrscheinlichkeiten bei dem Versuch berechnen:
- Wie groß ist die Wahrscheinlichkeit, die Zahl 3 zu Würfeln?
- Wie groß ist die Wahrscheinlichkeit, entweder eine 1 oder 4 zu Würfeln
Lösung
Wir wissen, dass der Würfel sechs gleiche Seiten hat. Somit können als Ergebnis beim Würfeln die Zahlen 1, 2, 3, 4, 5 oder 6 geworfen werden. Die Anzahl der möglichen Ergebnisse beträgt somit „6“. Kommen wir nun zu den drei Teilaufgaben:
- P({3}) = 1 : 6 = 0,1666…
- P({1, 4}) = 2 : 6 = 0,33333…
Historische Bemerkungen
Statistik: „Ich würfle n mal und berechne….“ Verfahren, um empirische Daten zu gewinnen, darzustellen, zu verarbeiten, zu analysieren, ..
Wahrscheinlichkeitstheorie: „Ich sage für die Zukunft voraus….“ Bestimmung eines Maßes für den Grad der Möglichkeit des Eintreffens noch unverwirklichter Ereignisse.
Stochastik: „Mathematik des Zufalls“, Sammelbegriff für die Gebiete Statistik und Wahrscheinlichkeitstheorie
Die häufigsten Fehler beim LaPlace Experiment
Haben wir es also tatsächlich mit einem LaPlace Experiment zu tun, können alle Ergebnisse mit der gleichen Wahrscheinlichkeit folgen. Dabei spielt uns vor allen Dingen die menschliche Intuition ein Schnippchen. Wirfst du zum Beispiel eine Münze, entspricht die Menge der Ergebnisse Omega: KK, KZ, ZK, ZZ. Diese Ereignisse besitzen die gleiche Wahrscheinlichkeit.
Ist einem Spieler die Reihenfolge herzlich egal, verändert sich auch die Menge der Ergebnisse zu: KK KZ ZZ – das Ergebnis KZ trifft mit doppelter Wahrscheinlichkeit zu? Werfen wir also eine Münze 2 Mal, können wir dies noch recht schnell erkennen. Bei anderen Experimenten ist das gar nicht mehr so übersichtlich.
Vollkommen durcheinander gerät unsere Logik, wenn eine Familie mit zwei Kindern in das Münzexperiment einsteigt und damit beginnt, jeweils die Münzen zu werfen. Klar, es steht 50 zu 50, ob nun das erste oder zweite Kind beginnt die Münze zu werfen. Dabei ist aber die Wahrscheinlichkeit für Mädchen und Junge doppelt so hoch zu berechnen.
Aus diesem Grund solltest du von Anfang an genauestens nachdenken, ob die Ergebnisse mit der gleichen Wahrscheinlichkeit auftreten. Bei berechtigten Zweifeln kann ein Baumdiagramm weiterhelfen.
Fazit zum LaPlace Experiment
Im Prinzip müssen wir davon ausgehen, dass es in der Realität eigentlich keines der LaPlace Experimente gibt, da die Wirklichkeit immer von der Theorie abweicht. Wir haben es hier mit reinen Zufallsexperimenten zu tun, bei denen alle Ergebnisse mit der gleichen Wahrscheinlichkeit auftreten. So ist davon auszugehen, dass es sich bei der Münze und dem Würfel, um den Willen einer Person im Raum und um ein LaPlace Experiment handelt.
