Lineare Funktion durch 2 Punkte
Die Funktionsgleichung einer linearen Funktion in Normalform lautet f(x)= y=mx+n
Dabei ist m die Steigung und n der y-Achsenabschnitt.
Zusammenfassung und Vorgehensweise
(zwei Punkte gegeben)
♦Steigung m mit Hilfe der Steigungsformel berechnen
♦Steigung m sowie die Koordinaten eines der beiden Punkte P(x|y) in die Normalform einsetzen und nach n auflösen
♦Funktionsgleichung aufstellen
Formel
f(x)= y=mx+n
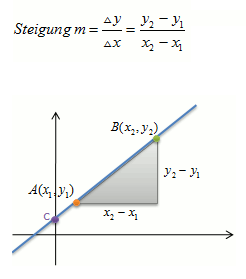
Formel für die Steigung
Unser Lernvideo zu : Lineare Funktion durch 2 Punkte
Steigung m
Die Steigung a gibt an wie steil die Gerade verläuft. Der Wert der Steigung gibt an um wieviel der y-Wert wächst wenn der x-Wert um 1 erhöht wird.
♦Ist m > 0 spricht man von einer steigenden Gerade
♦Ist m = 0 spricht man von einer x-Achsenparallelen Gerade
♦Ist m < 0 spricht man von einer fallenden Gerade y-Achsenabschnitt
Das b gibt den y-Achsenabschnitt an. Dies ist der Schnittpunkt mit der y-Achse. Man kann mit diesem Parameter die lineare Funktion nach unten oder oben verschieben. Mit einem positiven Wert verschiebt man die Funktion nach oben, mit einem negativen Wert nach unten.
y-Achsenabschnitt
Das b gibt den y-Achsenabschnitt an. Dies ist der Schnittpunkt mit der y-Achse. Man kann mit diesem Parameter die lineare Funktion nach unten oder oben verschieben. Mit einem positiven Wert verschiebt man die Funktion nach oben, mit einem negativen Wert nach unten.
Beispiel
Unsere Punkte sind P1 (2 / -2) und P2 (3/4)
Berechnung der Steigung m mit der Formel
![]()
⇒Nun wissen wir schon mal die Steigung der Funktion y = -2 x + t
⇒Jetzt berechnen wir den Schnittpunkt mit der y-Achse= n
Wir nehmen uns den Punkt P1 ( 2/-2)
wir setzen den x bzw y-Wert des Punktes in die unvollständige Funktionsgleichung ein
y= -2x+n
-2= -2*(2) +n
-2= -4 + n / +4
2=n
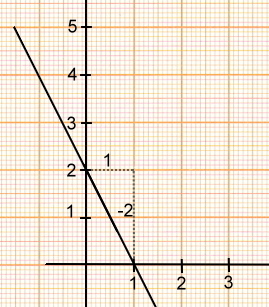
Unsere Funktionsgleichung lautet somit y= -2x + 2
Zeichnerisch würde das ganze dan so aussehen