Schnittpunkt zweier linearer Funktionen bestimmen
Hier erläutern wir wie man den Schnittpunkt zweier linearer Funktionen bestimmt.
Unser Lernvideo zu : Schnittpunkt zweier linearer Funktionen bestimmen
Beispiel zu: Schnittpunkt zweier linearer Funktionen bestimmen
Gegeben sind zwei lineare Funktionen:
f(x) = 0,5 • x + 2
g(x) = 3 • x – 3
Wir wollen nun den Schnittpunkt der beiden Funktionen bestimmen. Wir wollen also den x-Wert ermitteln an dem beide Funktionen denselben y-Wert haben. Alles was wir dafür machen müssen ist die beiden Funktionen gleichsetzen:
f(x)=g(x)
In diesem Beispiel bedeutet das:
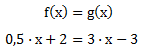
Jetzt können wir die Gleichung nach x auflösen. Wir sortieren das x nach links und alle anderen Teile nach rechts:
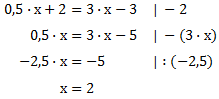
Wir wissen also nun, das der Schnittpunkt bei x = 2 liegt. Um den y-Wert des Schnittpunkts zu bestimmen, setzen wir den x-Wert einfach in eine der beiden Funktionen ein. Welche wir nehmen ist egal, da beim Schnittpunkt beide Funktionen denselben y-Wert besitzen. Wir setzen in die Funktion f(x) ein und können statt f(x) auch f(2) schreiben, da wir für x 2 einsetzen.
![]()
Zur Kontrolle setzen wir auch noch einmal in die Funktion g(x) ein:
![]()
Wir sehen also, dass beide Funktionen an der Stelle x = 2 einen y-Wert von y = 3 haben. Der Schnittpunkt liegt also bei P(2/3).
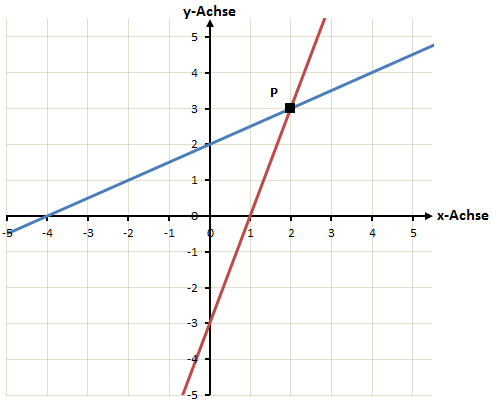
Hier noch einmal die grafische Darstellung. Auch hier sehen wir, dass der Schnittpunkt bei P(2/3) liegt.
Parallele Funktionen
Wenn zwei Funktionen parallel zu einander sind, haben sie natürlich keinen Schnittpunkt. Wir erkennen parallele Funktionen sehr gut daran, dass sie dieselbe Steigung a haben. Wir können es aber auch rechnerisch erkennen.
Beispiel
Bestimme den Schnittpunkt von den beiden Funktionen:
![]()
Wir setzen die Funktionen gleich und formen sie um:
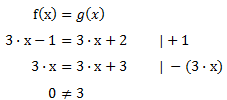
Wir können keinen x-Wert ermitteln, da es keinen Punkt gibt an den beide Funktionen denselben Funktionswert haben. Das Ergebnis ist daher „0≠3“ . Die Funktionen haben also keinen Schnittpunkt.
