Zeichnen von linearen Funktionen
Um eine Funktion zu Zeichnen braucht man üblicherweise eine Wertetabelle. Anschließend kann man die Punkte einzeichnen und verbinden. Bei einer linearen Funktion benötigen wir zum Zeichnen nur zwei Punkte, da wir wissen, dass die Funktion linear (also gerade) verläuft. Wir können also einfach zwei Punkte einzeichnen und diese dann mit einem Lineal verbinden.
Noch einfacher wird es, wenn wir uns überlegen, dass wir in der Funktionsvorschrift ja bereits die Steigung und den y-Achsenabschnitt gegeben haben. Diese beiden Werte können wir natürlich nutzen, wenn es um das Zeichnen einer linearen Funktion geht. Wir können den y-Achsenabschnitt also direkt in unser Koordinatensystem eintragen. Anschließend können wir uns mit Hilfe des Steigungsdreiecks die Steigung der Geraden überlegen.
Beispiel Zeichnen von linearen Funktionen
Wir zeichnen die Funktion f(x) = 2 • x + 1.
Wir wissen bereits, dass der y-Achsenabschnitt gleich 1 ist und die Steigung gleich 2 ist. Die Funktion schneidet die y-Achse also bei y=1. Wir zeichnen zunächst also einen Punkt bei x = 0 und y = 1.
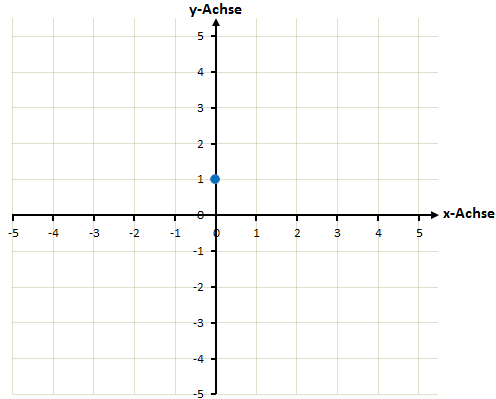
Nun zeichnen wir von diesem Punkt ausgehend das Steigungsdreieck. Wir gehen also einen nach rechts und 2 nach oben (da die Steigung ja gleich 2 ist):
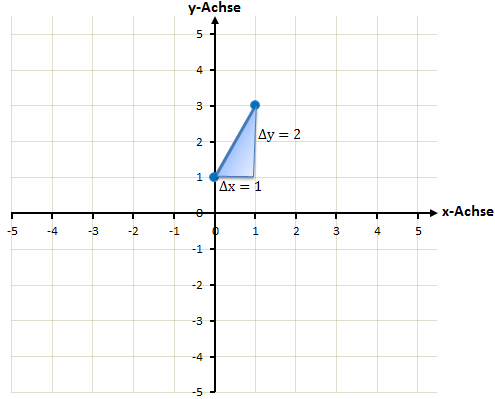
Jetzt haben wir bereits zwei Punkte und können so die lineare Funktion zeichnen. Wir können das Vorgehen aber auch wiederholen und erhalten so noch weitere Punkte die uns das genaue Zeichnen der Funktion erleichtern. Wir können dabei nach links und nach rechts vorgehen.
Nach rechts gehen wir immer ein Feld nach rechts und zwei nach oben und nach links gehen wir ein Feld nach links und zwei nach unten.
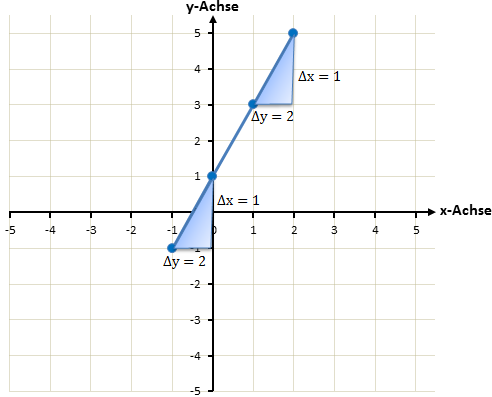
Sobald wir genug Punkte haben um die Gerade gut zeichnen zu können, zeichnen wir mit einem Lineal den fertigen Graphen:
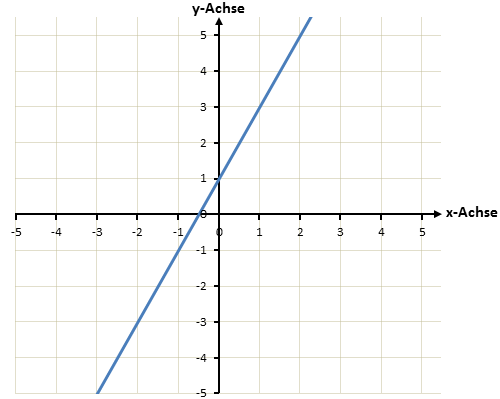
Das Vorgehen mit der Wertetabelle
Natürlich können wir aber auch ganz klassisch mit einer Wertetabelle vorgehen. Auch hierfür noch einmal ein
Beispiel
Wir zeichnen die Funktionen:
- f(x) = 2 • x
- g(x) = 2 • x + 2
- h(x) = 2 • x – 2
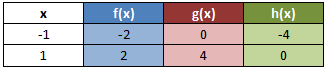
Dafür erstellen wir für jede Funktion eine Wertetabelle. Wir können diese Wertetabellen in einer Tabelle zusammenfassen. Dann sparen wir ein wenig Zeit und das Ganze ist ein bisschen übersichtlicher. Wir schreiben also in die erste Spalte die x-Werte und in die weiteren Spalten die y-Werte der jeweiligen Funktion.
Die y-Werte berechnen wir dabei mit den oben genannten Formeln. Für die Funktion f(x) lautet diese: f(x) = 2 • x. In der ersten Zeile rechnen wir also 2 • (-1) = -2 und in der zweiten Zeile 2 • 1 = 2. Genauso verfahren wir mit den Funktionen g(x) und h(x).
Anschließend können wir die Funktionen zeichnen. Wir zeichnen alle Funktionen in ein Koordinatensystem um sie besser vergleichen zu können. Wir Zeichnen also nacheinander die Funktionen f(x), g(x) und h(x) und beschriften diese entsprechend.
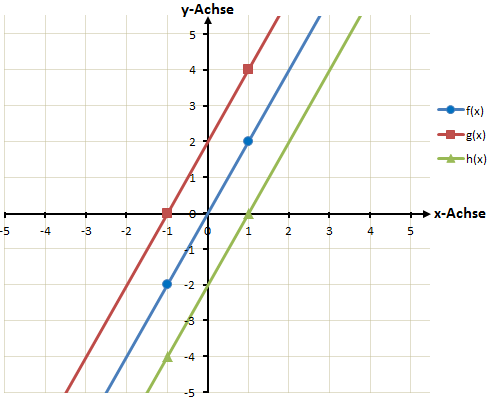
Wir können diese drei Funktionen nun gut vergleichen. Es handelt sich um 3 lineare Funktionen mit derselben Steigung. Sie sind also parallel zueinander aber jeweils nach oben oder unten verschoben.
