Innenwinkelsatz
Der Innenwinkelsatz des Dreiecks besagt, dass die Winkel im Dreieck immer 180° gemeinsam haben. Man drückt dieses mit der Rechnung α + β + γ = 180° aus. Mit dieser Rechnung kann man bei zwei bekannten Winkeln überprüfen wie groß der letzte ist. Auch wissen wir durch diesen Satz, dass die Winkelinnensumme eines Dreiecks niemals größer ist als 180°.
Nun wollen wir uns einmal ansehen, wie man zu dieser Behauptung kommt und nachprüfen, wie dieses bewiesen werden kann.
Um den Beweis anzutreten, brauchen wir die Nebenwinkel und Wechselwinkel, die ihr bereits kennengelernt habt. Gerne könnt ihr diese auch nochmal auf unserer Homepage nachlesen. Wir werden sie hier nocheinmal kurz einreißen.
Zur Erinnerung
Nebenwinkel entstehen, wenn zwei Geraden oder Strecken sich schneiden oder aufeinander treffen. Am Schnittpunkt entstehen Winkel. Die beiden Winkel nebeneinander ergeben summiert 180°, somit gilt: α + β = 180°.
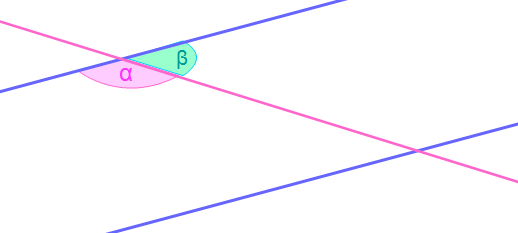
Wechselwinkel hingegen sind die selben Winkel auf der gegenüberliegenden Seite. Bei zwei Parallelen und einer schneidenden Gerade entstehen mehrere Winkelpaare. Somit auch Wechselwinkel, die die selbe Größe haben. In der unteren Abbildung seht ihr ein Beispiel für Wechselwinkel. Winkel β liegt auf der gegenüberliegenden Seite und hat die selbe Größe. Dieses ist durch die beiden blauen Parallelen entstanden.
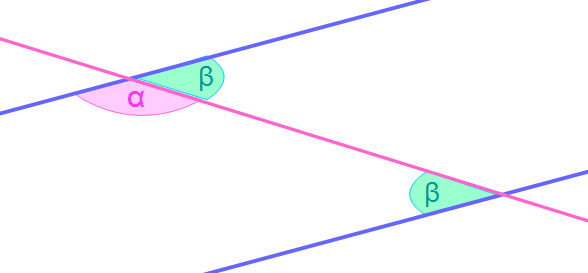
Gerne könnt ihr auf mathe-lerntipps.de mehr zu Winkelpaaren erfahren und nachlesen.
Unser Lernvideo zu : Innenwinkelsatz
Beweis des Innenwinkelsatzes
Nun nutzen wir unser bisheriges Wissen über Neben- und Wechselwinkel um zu beweisen, dass ein Dreieck immer die Innenwinkelsumme von 180° hat.
Wie sehen uns zunächst ein allgemeines Dreieck, mit den Eckpunkten ABC und den Winkeln α, β, γ, an.
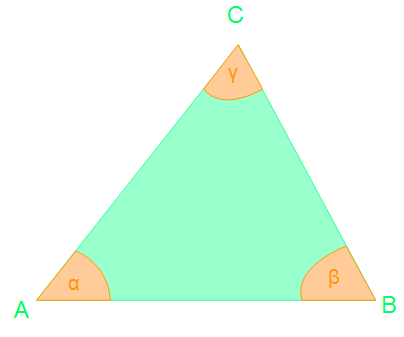
In dem abgebildetem Dreieck findet ihr die allgemeinen Punkte und Winkel. Leider sind uns keine Größen oder andere Maße gegeben, so dass wir die Winkelsumme nicht nachrechnen können. Daher bedienen wir uns einer anderen Variante, die wir bereits kennen und zwar der der Neben- und Wechselwinkel.
Für die beiden Winkelpaare benötigen wir zwei Parallelen. In einem Dreieck sind niemals zwei Seiten parallel, daher zeichnen wir uns eine Hilfslinie ein. Wir können zu jeder der Seiten eine Parallele zeichnen, wir nehmen die Parallele zur Seite AB und diese muss durch den Punkt C laufen, um den Winkel γ nutzen zu können.
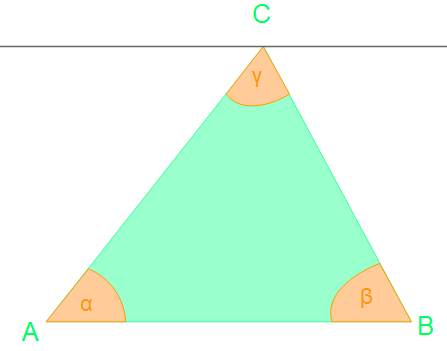
Es läuft eine Hilflinie durch den Punkt C. Sie ist parallel zur Seite AB. Wie ihr vielleicht direkt erkennen könnt, bilden sich an dem Punkt C zwei neue Winkel, die vom Dreieck zur Hilfsgeraden führen.
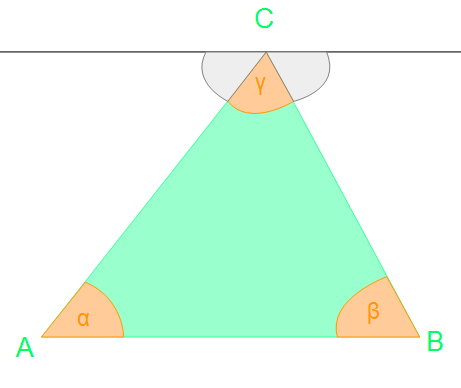
Nun haben wir die beiden neu entstandene Winkel nochmals markiert. Und nun kommen die Winkelpaare, die wir oben besprochen haben zum Einsatz. An der Hilfsgeraden stößt der Winkel γ und die zwei neuen Winkel. Durch das Prinzip der Nebenwinkel wissen wir, dass alle drei Winkel gemeinsam 180° ergeben.
Durch den Satz der Wechselwinkel wissen wir, dass rechts des Winkels γ der Winkel eben so groß ist wie α und der Winkel links ist genauso groß wie β. Somit können wir diese Bezeichnungen einsetzen:
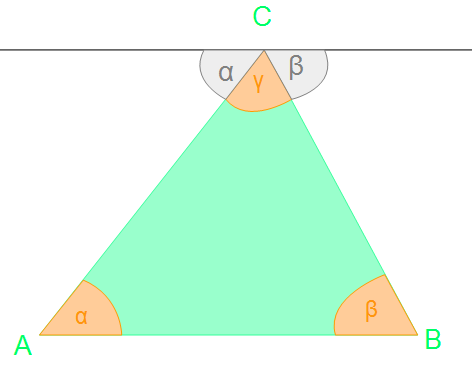
Nun haben wir alle Bezeichnungen mit dem bekannten Wissen eingesetzt. Wir wissen an der Hilfsgeraden durch den Punkt C sind alle Winkel 180° also α + β + γ = 180°. Da diese Winkel durch das Prinzip der Winkelpaare aus dem Dreieck übertragen wurden, können wir für das Dreieck die Behauptung aufbauen, dass die Innenwinkel immer α + β + γ = 180° ergeben. Der Beweis ist abgeschlossen.
