Allgemeines Dreieck
Ein Dreieck ist eine geometrische Figur und das einfachste Polygon (Vieleck). Wir betrachten hier das allgemeine oder auch unregelmäßiges Dreieck genannt.
Jedes Dreieck hat folgende Eigenschaften:
– Drei Punkte, die nicht auf einer Geraden liegen. Diese werden Ecken genannt.
– Drei Verbindungsstrecken zwischen je zwei Punkten. Diese werden Seiten genannt.
Schritt für Schritt – Anleitung
Nun nehmen wir uns das Dreieck geometrisch vor.
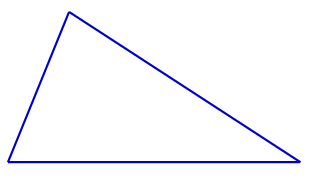
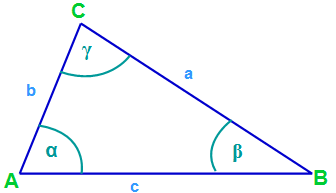
Wir sehen ein beliebiges Dreieck. Es hat drei Ecken und drei Seiten.
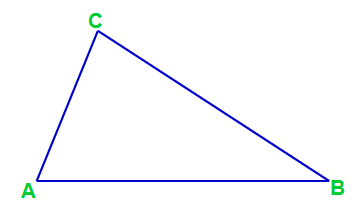
1. Schritt: Als erster Schritt werden die Eckpunkte beschriftet. Dazu verwendet man immer großgeschriebene Buchstaben und im Normalfall immer A, B und C. Nur sehr selten werden andere Großbuchstaben genutzt, so dass wir auch bei der üblichen Handhabung bleiben.
Zu beachten ist, dass man sich den Eckpunkt A beliebig aussuchen kann, dann aber gegen den Uhrzeigersinn beschriftet.
2. Schritt: Nun werden die Seiten beschriftet. Hier nutzt man kleingeschriebene Buchstaben.
Dabei zu beachten ist, dass man die Seite gegenüber eines Eckpunktes mit dem gleichen Buchstaben versieht, jedoch kleingeschrieben. Daher nutzt man die Seitenbeschriftung a,b und c.
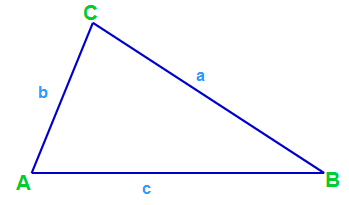
Wie an dem obigen Dreieck zu sehen, liegen die Seitenbezeichnungen gegenüber den Eckpunkten. c gegenüber C, a gegenüber A und b gegenüber B.
3. Schritt: Nun werden die Innenwinkel eingetragen. Dazu nutzt man den griechischen Buchstaben des Eckpunktes:
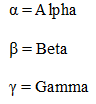
Zunächst wird ein kleiner Bogen im inneren Dreieck am jeweiligen Eckpunkt gezeichnet oder der griechische Buchstabe eingefügt.
Somit ist die Beschriftung des Dreiecks vollendet.
Unser Lernvideo zu : Allgemeines Dreieck
Weitere Eigenschaften eines Dreiecks
– Die Summe der Innenwinkel beträgt bei jedem planaren (ebenen) Dreieck 180°.
![]()
– Die Addition zweier Seitenlängen ist stets länger (oder gleich lang) als die dritte Seite des Dreiecks. Dies nennt man die Dreiecksungleichung.
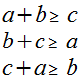
Mit den nun bekannten Eigenschaften, kann man viele Dreiecke zeichnen und errechnen, auch wenn man nicht alle einzelnen Größen kennt und z.B. eine Seitenlänge fehlt. Genaue Erklärungen dazu findet ihr unter dem Punkt „Kongruenzsätze und Konstruktion“.
