Anwendung des Thaleskreises
Bisher haben wir den Thaleskreis kennen gelernt, ihn bewiesen und wissen, wie wir ihn konstruieren können. Nun ist es natürlich wichtig, dass wir ihn auch anwenden lernen. Denn genau das, ist ja auch der Knackpunkt im Unterricht.
Ihr werdet in der Schule verschiedene Aufgaben gestellt bekommen, einige einfache, aber auch knifflige, bei denen ihr um zwei Ecken denken müsst. Der Trick beim Lösen von Aufgaben ist es nicht, auf Anhieb die Lösung zu wissen und hin zu schreiben, sondern, man sucht was gegeben ist und schaut dann, wie man mit seinem eigenen Wissen nächer an die Lösung kommt und manchmal hat man sie dann ganz automatisch. Wichtig ist, sich nicht schlecht zu fühlen, nur weil einem nicht sofot ein Licht aufgeht. Lieber das eigene Wissen ruhig anwenden und langsam weiter heran tasten.
Hier werden wir nun ein paar Aufgaben durchgehen.
Übung 1
Richtig oder Falsch?
1. Die Ecken eines rechtwinkligen Dreiecks in einem Thaleskreis haben alle den selben Abstand zum Mittelpunkt des Kreises?
2. Zu jedem rechtwinkligem Dreieck gehört ein Thaleskreis?
3. Jedes Dreieck auf dem Thaleskreis hat immer γ = 90°?
4. Der Durchmesser des Thaleskreises ist auch der Radius?
5. Die Höhe eines Dreiecks im Thaleskreis ist genausolang wie die Strecke MC?
Antworten:
zu 1: Richtig. Denn die Ecken haben alle den Abstand gleich dem Radius, der vom Mittelpunkt aus geht.
zu 2: Richtig. Denn man kann immer die Hypothenuse des Dreiecks als Durchemesser des Kreises nehmen und und dann liegt der Eckpunkt mit dem rechten Winkel auf dem Thaleskreis.
zu 3: Falsch. Es ist nicht unbedingt nötig dass der rechtwinklige Eckpunkt C ist. Denn bezeichnen kann man die Ecken ja, wie man möchte, solange man im Uhrzeiger Sinn geht.
zu 4: Falsch. Der Durchmesser ist natürlich immer das doppelte vom Radius!
zu 5: Falsch. Die Höhe eines Dreiecks ist immer von der Grundlinie senkrecht hoch zum Eckpunkt. Wenn C nun nicht genau über M liegt, verschiebt sich die Höhenlinie.
Übung 2
Winkel gesucht
Finde heraus, wie groß die markierten Winkel sind.
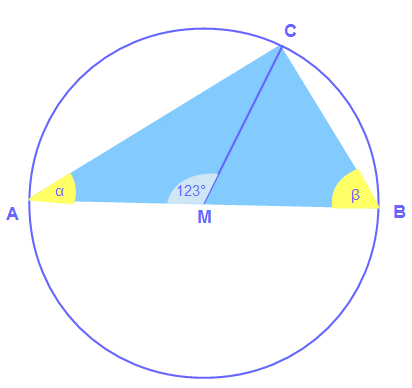
Antwort:
α = 28,5°
β = 61,5°
Erklärung: Hier machen wir uns die Begebenheiten des Thaleskreis zur Nutze.
Als erstes wollen wir α herausfinden. Unser Dreieck ist nun AMC, welches, durch den Thaleskreis ein gleichschenkliges Dreieck ist. Das bedeutet, dass die Winkel der Basis gleich groß sind und dass die Innenwinkel insgesamt 180° betragen. nun können wir einfach rechnen: 180° -123° = 57°. Das bedeutet, dass die beiden noch unbekannten Winkel in AMC zusammen 57° betragen, da sie gleich groß sind, rechnen wir: 57°: 2 = 28,5°
Als nächstes berechnen wir β. Wir kennen α = 28,5° und γ = 90°. So können wir nun die Innenwinkel des Dreiecks ABC berechnen: 180° – 90° – 28,5° = 61,5°.
Eine andere Variante ist die, dass wir wissen, das γ = 90° ist. Dieses Winkel haben wir mit der Strecke MC geteilt. Die eine Hälfte des geteilten Winkels ist 28,5°. Somit ist die andere Hälfte 90° – 28,5° = 61,5°. Da auch das Dreieck MBC ein gleischenkliges ist, sind die Winkel an der Basis gleich groß und somit ist auch β = 61,5°.
Übung 3
Konstruktion einer Kreistangente
Diese Aufgabe ist eine klassische Aufgabe in Bereich des Thaleskreises und eine bei der man einmal um die Ecke denken muss, um aufs Ergebnis zu kommen.
Gegeben ist ein Kreis mit dem Mittelpunkt M und ein Punkt P, der außerhalb des Kreises liegt. Nun soll eine Tangente am Kreis durch den Punkt P gezeichnet werden.

Nun sehen wir uns zunächst an, was wir wissen. Wir kennen M und P. Und wir wissen, dass eine Tangente t einen Kreis nur in einem Punkt T berührt. Um dies gewährleisten zu können, muss die Strecke MT senkrecht zur Tangente t liegen. Und an dieser Stelle nutzen wir den Thaleskreis aus.
Wir wissen, dass jeder Punkt auf einem Thaleskreis ein rechtwinkliges Dreieck mit den Endpunkten des Durchmessers ergibt. Zwei Punkte sind uns bereits gegeben M und P, welche wir als Endpunkte nutzen können. Somit zeichnen wir als ertes die Strecke MP ein.
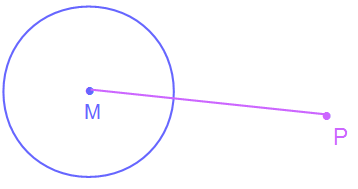
Nun haben wir eine Strecke MP in unserer Abbildung. Durch den Satz des Thales wissen wir, dass wenn wir nun um diese Strecke einen Kreis ziehen jeder Punkt auf dem Kreis ein rechtwinkliges Dreieck mit den Punkten M und P bildet. Daher zeichnen wir als nächstes einen Kreis mit MP als Durchmesser.
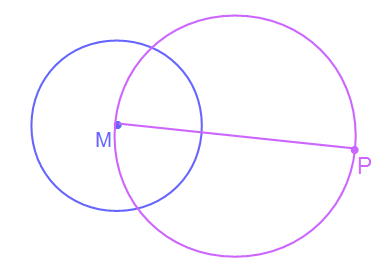
Wir sehen den eigezeichneten Kreis mit dem Durchmesser MP. Der neue violette Kreis schneidet den Ausgangskreis in zwei Punkten. Beide Schnittpunkte ergeben laut dem Satz des Thales ein rechtwinkliges Dreieck. Wir zeichnen hierzu mal eines ein. Welches ist egal, dies gilt nur der Demonstration.
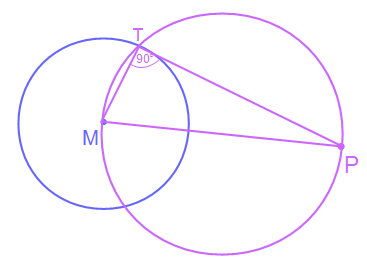
Wir sehen das Dreieck MPT. Dieses ist rechwinkling im Eckpunkt T. Dies bedeutet wiederum, dass die Strecke MT senkrecht zur Strecke PT ist und somit haben wir unseren Punkt der Kreistangente gefunden. Verlängern wir nun die Strecke PT, dann haben wir unsere Kreistangente t.
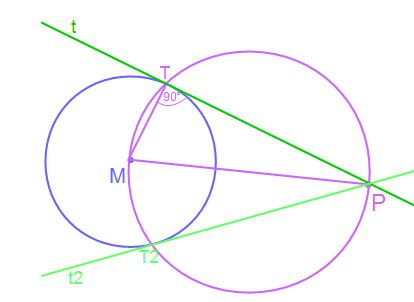
Nun sehen wir das Ergebnis unserer Aufgabe. Zunächst die grüne Tangente t, die durch die Punkte T und P läuft und senktrecht zu MT ist.
Da wir aber zwei Schnittpunkte der Kreise hatten, haben wir auch zwei mögliche Tangente. die weite ist in einem etwas hellerem grün eingezeichnet und wird genauso ermittelt wie die erste.
Somit haben wir einige mögliche Anwendungen des Thalessatzes erkundet und können uns allen anderen Übungen stellen.
