Kreisteile
Nun wollen wir euch beschreiben und zeigen, was Kreisteile sind und wie wir sie berechnen. Ein Kreisteil wird auch Kreisausschnitt genannt und ist ein Teil eines ganzen Kreises. Zu berücksichtigen ist dabei der Radius des Kreises und der Kreisbogen des Kreisausschnitts.
Was ist ein Kreis?
Wir haben es bei einem Kreis mit einer Kurve und einem eindimensionalen Gebilde zu tun. Wobei wir zwischen den offenen und abgeschlossenen Kreisflächen unterscheiden.
Was sind Kreisteile?
Eigentlich verstehen wir darunter nichts anderes als Figuren, die sich aus Kreisbögen zusammensetzen. Diese Figuren lassen sich anhand der Ecken und Bögen neu ordnen. Wobei an einer Ecke nur zwei Kreisbögen aufeinandertreffen.
Die Berechnung einer Kreisfläche und Kreisringe haben wir bereits behandelt. Gerne könnt ihr euch dieses nochmals auf dieser Homepage unter dem Punkt Flächeninhalt eines Kreises nachlesen. Dieses benötigen wir als Grundlage zur Berechnung von den Flächeninhalten von Kreisausschnitten und der Länge des Kreisbogens.
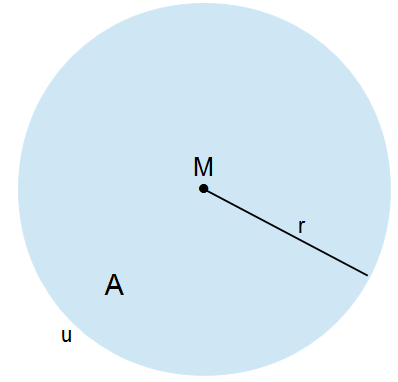
Wir gehen wir von einem allgemeinen Kreis aus. Dieser hat einen Mittelpunkt M, einen Radius r. Der Radius hat immer die selbe Länge vom Mittelpunkt zum Rand des Kreises. Desweitern kennen wir noch Umfang u und die Flächeninhalt des Kreises A.
Zur Erinnerung
Wir wollen nochmals die Formeln aufstellen, die wir für die Berechnung des Umfangs und des Flächeninhalts eines Kreises benötigen.
Umfang: u = 2π r
Flächeninhalt: A = π r2
Kreisausschnitt
Zwei Radien eines Kreises teilen die Kreisfläche in zwei Kreisausschnitte. Diese Kreisteile haben jeweils einen dazugehörigen Kreisbogen. Die Länge des Kreisbogens b ist proportional zum Winkel des Kreisteils am Mittelpunkt des Kreises. Dieser wird Mittelpunktswinkel α genannt. Weil die Läng des Kreisbogen proportional zum Mittelpunktswinkel ist, ist auch der Flächeninhalt des Kreisausschnitts proportional zum Winkel. Das bedeutet vereinfacht gesagt, je größer der Winkel, desto größer die Kreisbogenlänge und der Flächeninhalt des Kreisausschnitts.
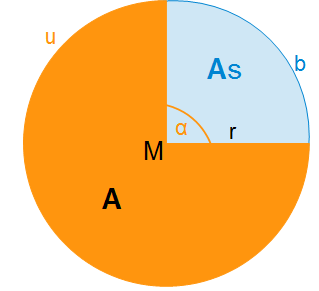
In der Abbildung seht ihr einen Kreis, der mit der mit zwei Radien in zwei Kreisteile geteilt wurde, einen orangen und einen blauen Kreisteil. Beide Kreisteile haben einen Kreisbogen, der anhängig vom Winkel am Mittelpunkt ist.
Formeln
Die bisherigen Formeln zur Kreisberechnung sind uns bekannt. Dazu gehört einmal die Berechnung des Kreisumfangs und zum anderen die Berechnung der Kreisfläche. Um die Kreisausschnitte und deren Bögen zu ermitteln, nutzen wir die uns bekannten Formeln. Da beide proportional zum Mittelpunktswinkel α sind, können wir diese in Abhängigkeit stellen. Daraus folgen folgende Formeln:
Für die Bogenlänge:
![]()
Die Basis liegt auf der Umfangsformel eines Kreises. Als nächstes stellen wir den Bezug zwischen der Bogenlänge und dem Mittelpunktswinkel auf, setzen ein und formen um:
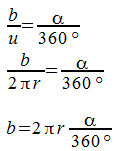
Somit haben wir die Formel für die Bogenlänge ermittelt. Nun können wir mit jedem Mittelwinkel die Bogenlänge des Kreisaussschnittes berechnen.
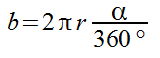
Für den Flächeninhalt:
![]()
Auch hier liegt die Basis auf dem Flächeninhalts eines Kreises. Nun setzen wir den Flächeninhalt des Kreises in Bezug zum Mittelpunktswinkel, setzen ein und formen um:
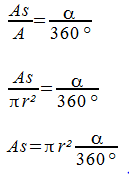
Somit haben wir die Formel für den Flächeninhalt eines Kreisausschnittes definiert und können sie zur Berechnung bei Kreisausschnitten nutzen.
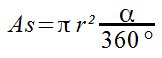
Wie haben wir Kreisteile vor Tausenden Jahren berechnet?
Im Grunde gehört der Kreis zu den ältesten Figuren in der vorgriechischen Geometrie. Wir sind schon seit mehr als 4.000 Jahren mit der Berechnung der Kreisteile beschäftigt.
- Zunächst bestimmt man den Flächeninhalt A.
- Dabei subtrahiert man ein Neuntel der Länge mit dem Durchmesser d.
- Im Anschluss multipliziert man das Ergebnis noch einmal mit sich selbst.
- Diese annähernde Bestimmung der Kreisfläche können wir heute noch in der Papyrus Rhind wiederfinden.
Die Babylonier haben den Kreisumfang U genommen und davon ausgehend im Durchmesser eines Kreises d 3 Mal geschätzt. Um auf den Flächeninhalt zu kommen, hatten die Mathematiker damals 1/12 des Quadrats des Umfangs genommen. Im direkten Vergleich steigt die Abweichung, sodass sich diese Rechenformel nicht durchsetzte. Wobei es ihnen gelang, den Umfang genauer zu berechnen. Im Zuge der nächsten Jahrzehnte konkretisierten sich die Berechnungen und es entwickelten sich sehr genaue Formeln und Rechenwege.
Im Zusammenhang mit der analytischen Geometrie können wir anhand von Gleichungen, verschiedene Größen geometrischer Objekte berechnen. Dabei solltet ihr für die einzelnen Größen immer die passende Formel zur Hand haben, diese sind wiederum im Tafelwerk zu finden.
Interessante Fragen und Antworten zu Kreisteile
Welche formel muss ich benutzen un den umfang eines Kreises errechnen zu können? |
| Die Mathematik bietet uns sehr interessante Lösungsansätze und hält in der Regel für jedes Problem auch die passende Lösung bereit. Nun liegt es an jedem selbst die Formeln, die uns angeboten werden auch korrekt einzusetzen. Hier geht es jetzt um die Frage, welche Formel hilfreich bei der Kreiselberechnung ist?Es geht nicht darum, das Volumen des Kreisels zu berechnen oder auch die Füllung des Kreises. Es geht um den Umfang und die korrekte Berechnung und da gibt es nur eine passende Lösung. Der Nutzer kann nun folgende Formel benutzen und sollte diese auch mit seinen vorgegebenen Zahlen auffüllen.
U=2·?·r Diese Formel wird dann zeigen, was gebraucht wird. Aus der Aufgabe können nun diese Zahlen entnommen und eingesetzt werden. Die Lösung ist dadurch einen Schritt näher gekommen und es ist noch nie so einfach gewesen, auf das korrekte Ergebnis zu kommen. Der Nutzer kann sich natürlich auch helfen lassen und wird damit auf der sicheren Seite sein. Wichtig ist diese Aufgabe in der Regel ab der 10. Klasse und dann sollte sie auch korrekt eingesetzt werden. Mit dem Ergebnis richtig liegen ist immer wichtig und das sollte niemand vergessen. Wer alles richtig macht, kann dann auch eine gute Note bekommen. |
