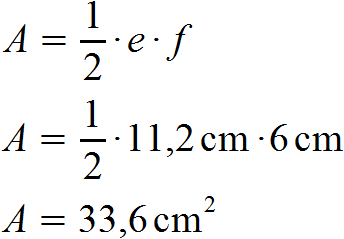Flächeninhalt eines Drachens
Ein Drachen, mathematisch korrekt auch Deltoid genannt, ist ein Viereck mit einer diagonalen Symmetrieachse.
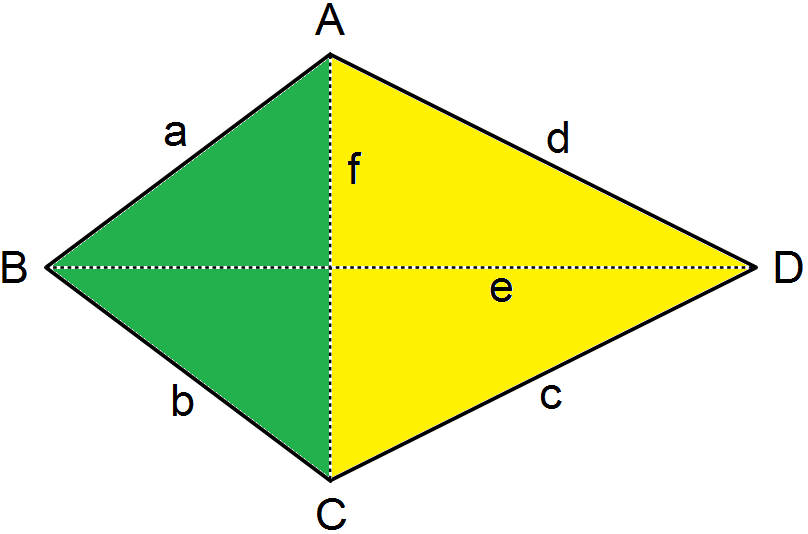
In unserer Darstellung verläuft diese Symmetrieachse entlang der Diagonalen e. Somit sind sowohl die Seiten a und b als auch c und d gleich lang. Zur Verdeutlichung der Symmetrie ist die Fläche hier farblich unterteilt worden. Der Drachen wird durch die Diagonalen e und f in vier kleinere Dreiecke unterteilt. Durch die Symmetrieachse bei e ergeben sich jeweils zwei deckungsgleiche Dreiecke, die in der Skizze grün bzw. gelb gekennzeichnet sind.
Die Fläche eines Drachens lautet wie folgt:
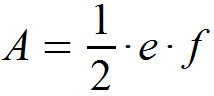
Lerntool zu Flächeninhalt eines Drachens
Unser Lernvideo zu : Flächeninhalt eines Drachens
Herleitung der Formel
Kennst du die Herleitung für die Formel einer Fläche, so kannst du sie dir auch besser merken. Die Herleitung für den Drachen ist relativ einfach und soll hier deshalb kurz erklärt werden.
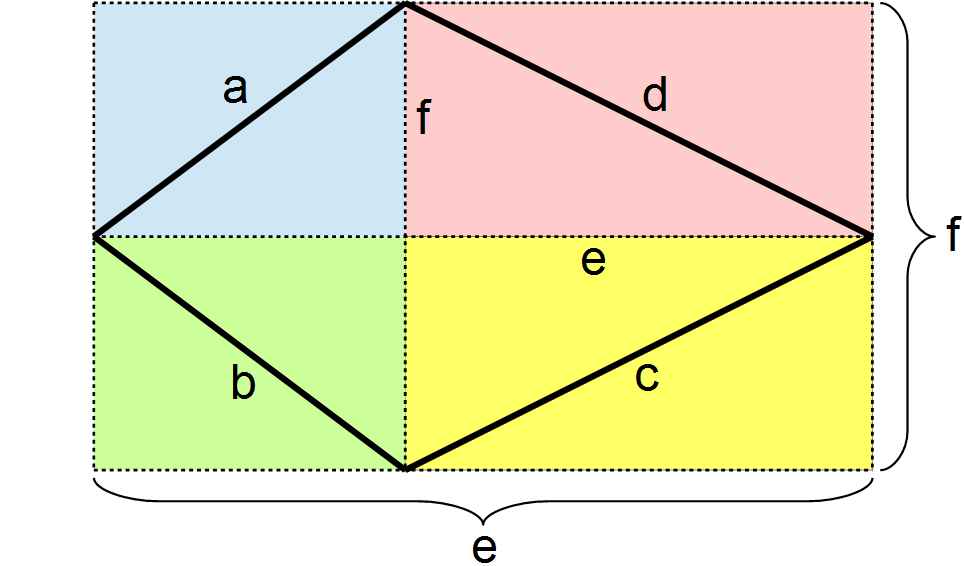
Schauen wir uns hierfür zunächst nochmals die Formel für die Fläche an.
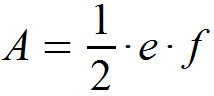
In der Formel taucht das Produkt aus den Diagonalen e · f auf. Hierdurch ergibt sich die Fläche eines Rechtecks, dass der gesamten farbigen Fläche in der Skizze entspricht und unseren Drachen exakt umschließt. Teilen wir nun dieses Rechteck in vier kleinere Rechtecke mit den Seiten des Drachens als Diagonalen und markieren sie jeweils mit unterschiedlichen Farben. Wie du siehst, setzt sich die Fläche des Drachens aus der Hälfte dieser vier kleineren Rechtecke zusammen.
Nehmen wir also die Hälfte der Fläche aus den Diagonalen e und f, erhalten wir die Fläche für unseren Drachen.
Beispiel
Die Fläche des folgenden Drachens soll berechnet werden.
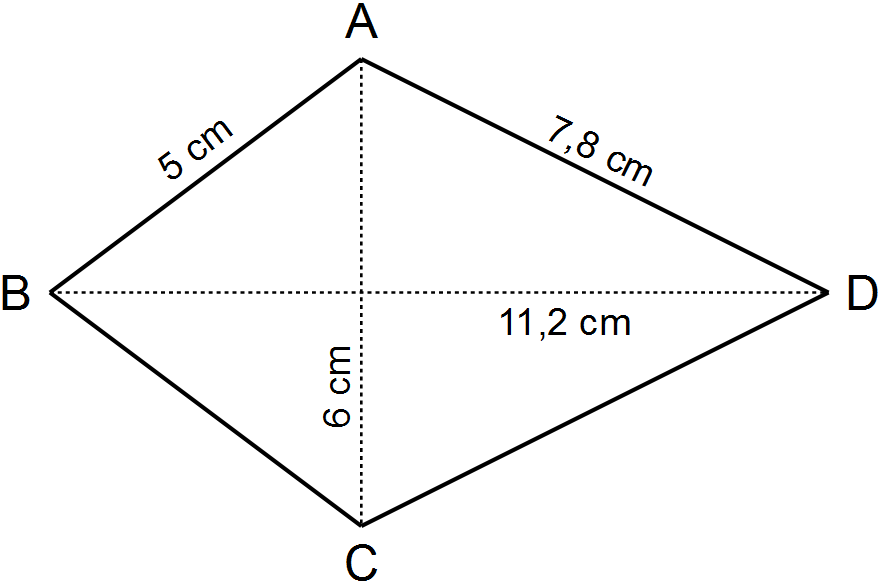
Mit Hinblick auf die Formel für die Fläche müssen wir zunächst die Diagonalen e und f identifizieren. Aus der Skizze entnehmen wir also folgende Werte:
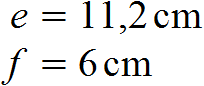
Mit diesem Wissen können wir bereits die Fläche berechnen und erhalten folgendes Ergebnis: