Produktregel zum Ableiten
Besteht die abzuleitende Funktion aus zwei Faktoren, die beide jeweils von x abhängen, so ist nach folgender Formel vorzugehen.
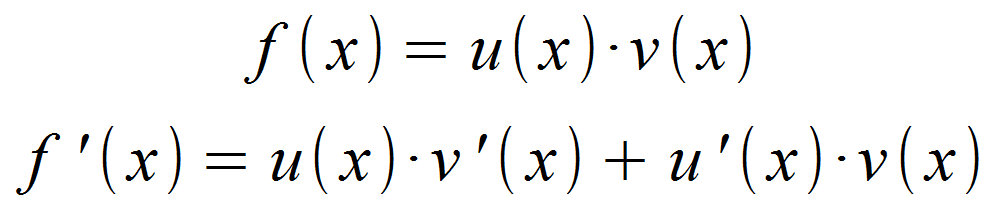
Hierbei geht man am besten folgendermaßen vor:
- u (x) und v (x) identifizieren
- u ‚(x) und v ‚(x) bilden
- in Formel für f ‚(x) einsetzen
- ausmultiplizieren und vereinfachen
Unser Lernvideo zu : Produktregel zum Ableiten
Beispiel
Folgende Funktion soll abgeleitet werden.
![]()
Wir identifizieren zunächst u(x) und v(x).
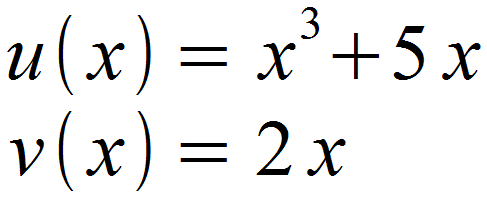
Daraufhin leiten wir diese ab.
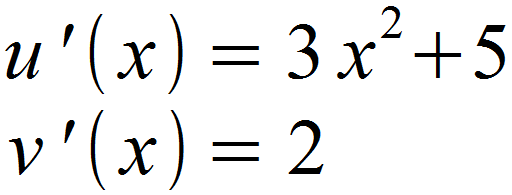
Im nächsten Schritt werden die erhaltenen Funktionen in die Formel für f ‚(x) eingesetzt.
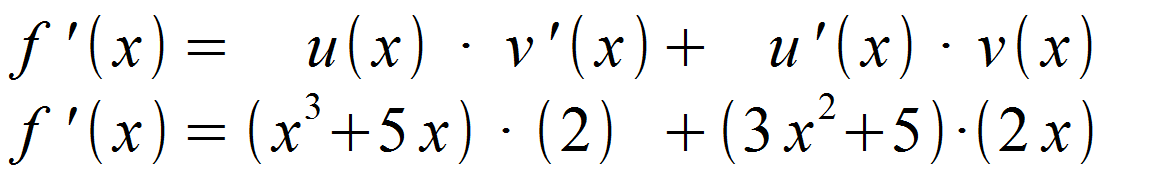
Wir multiplizeren aus und vereinfachen abschließend.
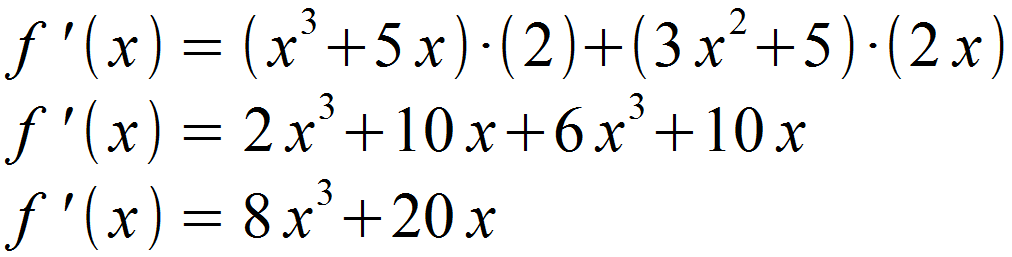

Alternativ hätte die Funktion auch nach vorangehendem Ausmultiplizieren mit der Summenregel gelöst werden können.
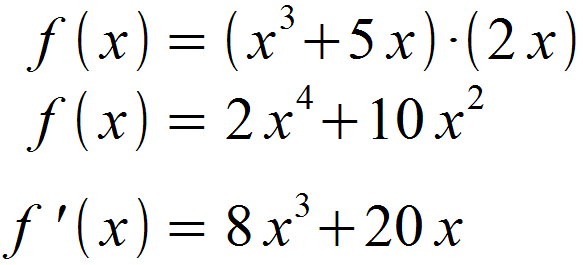
Dieser Weg mach hier vielleicht einfacher sein, oft führt an der Produktegel jedoch kein Weg vorbei.
