Aufleiten Produkt
Unter partieller Integration versteht man eine Methode, ein vorliegendes Integral auf ein anderes, einfacher zu berechnendes zurückzuführen. Da es dabei darauf ankommt, den Integranden in ein Produkt zweier Faktoren zu zerlegen und dann für den einen Faktor eine Stammfunktion anzugeben, bezeichnet man diese Integrationsmethode als partielle Integration. Die Produktintegrationsformel wird aus der Produktregel der Differenzialrechnung hergeleitet, deswegen nennt man die partielle Integration auch die Umkehrung der Produktregel
Technisch gesehen ist eine Stammfunktion:
Beispiel (x3)‘ = 3x2 ; aber auch (x3+4)‘ = 3x2 und (x3-8)‘ = 3x2 oder allgemein (x3+C)‘ = 3x2 ist für jede Zahl C. Jede Funktion besitzt demnach unendlich viele Stammfunktionen, aber alle unterscheiden sich nur um eine Konstante. Das merken wir uns „kennen wir eine Stammfunktion, kennen wir alle“
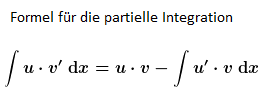
→Die Regel der Partiellen Integration ist also für f(x)· g(x) dann anwendbar, wenn man für F(x)· g’(x) eine Stammfunktion angeben kann – und natürlich F(x) kennt
Beachte: ‚Obergrenze‘ bezeichnet immer die Zahl, die im Integral oben steht. Auch falls sie kleiner als die Untergrenze sein sollte!
→statt „aufleiten“ sagt man meist „integrieren
Zusammenhänge zwischen f(x), f′(x) und F(x)
♦f(x) ist eine gegebene Funktion
♦f′(x) ist die Ableitung von f(x)
♦F(x) ist die Stammfunktion von f(x)
♦ f(x) ist die Stammfunktion von f′(x)
Beispiel
Für die folgende Funktion f(x)= ex *x soll eine partielle Integration durchgeführt werden.
Zuerst teilen wir auf
u(x)= x
v`(x)= ex
Jetzt setzen wir in die Formel ein
F(X)= u*v – ∫ ( u`*v) dx
F(X)= x* ex – ∫(1-ex) dx
F(X)=x*ex -∫ ex dx
F(X)= x*ex -ex +C Lösung!
