Obersumme und Untersumme Aufleitung
•Die Summe der Flächeninhalte der großen Rechtecke wird als Obersumme, die der kleinen als Untersumme bezeichnet.
•Je größer die Anzahl n der Rechtecke wird, umso genauer werden Ober- und Untersumme und umso kleiner wird deren Differenz. Es gilt aber immer: Untersumme U ≤ Fläche A ≤ Obersumme O
•Die Obersumme heißt nun deshalb Obersumme, da ein Stück des entstandenen Rechteckes über die Gerade hinausragt. Dies ist bei der Untersumme nicht der Fall. Die Ober- oder Untersumme errechnet sich nun als Summe der Flächen der einzelnen Abschnitte.
•Die Flächensumme der n dem Graphen einbeschriebenen Rechtecke der Breite heißt die ∆x Untersumme und die der umbeschriebenen Rechtecke U(n) die Obersummer der O(n) Funktion f auf [a; b]
•Bei der Bildung einer Untersumme entspricht die Länge jedes Rechtecks dem kleinsten Funktionswert von f im betrachteten Teilintervall. Wird die Obersumme gebildet, entspricht die Länge jedes Rechtecks dem größten Funktionswert von f im betrachteten Teilintervall.
Definition
Es sei f eine im Intervall [a; b] stetige reelle Funktion. Jene reelle Zahl, die zwischen allen Untersummen und allen Obersummen von f in [a; b] liegt, nennt man das Integral von f in [a; b] und bezeichnet diese Zahl mit
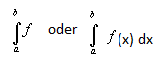
Ausgesprochen wird es: „Integral von f zwischen den Grenzen a und b“ oder „Integral von f von a bis b“. Die Funktion f wird Integrand genannt. Das Berechnen von Integralen nennt man Integrieren.
♦Flächeninhalte oberhalb der x-Achse haben ein positives Vorzeichen.
♦Flächeninhalte unterhalb der x-Achse haben ein negatives Vorzeichen.
Beispiel
Unter und Obersumme für die Funktion f(x)= x2/2
Breite der Teilintervalle : ∆x= b-a/2 = 2-0 /4 = 1/2 =0,5
Untersumme: ∆x* [ f(x0) + f( x1) + ….f( xn-1) ]
= 1/2 [f(0) + f(0,5) + (f(1)* (3/2) ]
=1/2 [ 0,5 *02 + 0,5*0,52 +0,5 *12 +0,5* 1,52 ]
= 0,875
Obersumme: ∆x* [ f(x1) + f( x2) + ….f( xn) ]
= 1/2 [ f(0,5) +f(1) +f( 3/2) * f(2) ]
=1/2 [ 0,5 *0,52 +0,5 *12+ 0,5*1,52 + 0,5 *22 ]
= 1,875
