Wurzelfunktion ableiten
- Wurzelfunktionen sind Spezialfälle von Potenzfunktionen.
- Wir können daher jede einfache Wurzelfunktion mit der Potenzregel ableiten.
- Jede Wurzel kann auch als Exponent geschrieben werden
![]()
Möchte man keine Wurzel von x ableiten, so benötigt man die Kettenregel. Es ergeben sich dann zwei Funktionen:
- Die äußere Funktion ist die Wurzel
- Die innere Funktion ist der Ausdruck, der unter der Wurzel steht (Radikand)
Unser Lernvideo zu : Wurzelfunktion ableiten
Beispiel 1
Unsere Funktion lautet f(x): √4x2+2x
Wir erstellen nun eine Tabelle
| Ausgangsfunktion | Ableitung | |
| äußere Funktion f |  |
 |
| innere Funktion g | 4x2+2x | 8x+2 |
Nun bilden wir die erste Ableitung
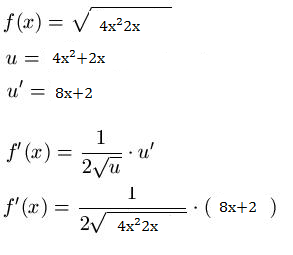
Bei der Kettenregel wird die äußere Funktion zuerst abgeleitet und vor die gesamte Ableitungsfunktion geschrieben. Danach wird die innere Funktion abgeleitet und mit der äußeren Ableitung multipliziert.
Bei der äußeren Ableitung wird das betrachtet, was außerhalb der Klammer bei f(x) steht
Bei der inneren Ableitung, wird das betrachtet, was innerhalb der Klammer bei f(x) steht
Merke: Der Wert unter der Wurzel, der sogenannte Radikand, darf nicht kleiner als null sein!
Beispiel 2
![]()
⇒Der Trick besteht darin, daß wir die Wurzel einfach als Potenz mit rationalen Exponenten schreiben
![]()
Merke
- Ableitung einer Konstante ist Null, z.B f(x)=6 ⇒ f(x)`= 6 ⇒ 0! ; denn Eine Konstante ist ein Term, welcher nicht die Ableitungsvariable enthält. die Ableitung einer Konstante ist immer 0
- Alle Funktionen haben Ableitungsfunktionen. Die Struktur der Funktion bestimmt dabei, welche Regeln man anwenden muss. Also muss man als erstes erkennen, welche Regel man braucht.
- Die Ableitung beschreibt die Steigung oder Änderungsrate ihrer Ausgangsfunktion.
- Jede Wurzel kann auch als Exponent geschrieben werden
