Integration durch Substitution
•Die Integration durch Substitution ist eine Methode zur Berechnung von Stammfunktion und Integralen.
•Integration durch Substitution Diese Integrationsmethode beruht auf der Kettenregel der Differentialrechnung.
Voraussetzungen
Steht in einem Integral die Verknüpfung von zwei Funktionen (evtl. sogar multipliziert mit der Ableitung der inneren Funktion), kann Substitution zur Vereinfachung beitragen.
Formel
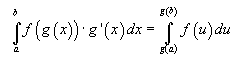
dabei ist u= g(x) ; du= g`(x)dx
Die Substitutionsregeln kann immer dann angewendet werden, wenn man beim Ableiten die Kettenregel verwenden würde. Ziel ist es, ein bestimmtes Integral über eine Standardfunktion zu erhalten, das nach der gängigen Methode berechnet wird: Stammfunktion finden – Integrationsgrenzen einsetzen – Werte voneinander abziehen.
Diese Regel bzw Formel ist in folgender Situation anwendbar:
• Der Integrand muss das Produkt zweier Funktionen sein.
• Von einem Faktor (g 0 (x)) muss man die Stammfunktion g(x) kennen
Bei der Integration durch Substitution wird die Integrationsformel von links nach rechts gelesen. Falls die Funktion g umkehrbar ist, kann man auch vom rechts stehenden Integral ausgehen und die Integrationsvariable z durch einen Funktionsterm g(x) in der neuen Variablen x ersetzen.
Ziel der Substitution ist es, den zu integrierenden Ausdruck zu vereinfachen: Der Integrand wird durch eine neue Variable ausgedrückt und umgeformt. Einfacher gesagt; bei der Integration durch Substitution führst du ein unbekanntes Integral auf bekannte Beispiele zurück und kannst somit komplizierte Terme in einem Integral vereinfachen
Merke :Du musst die Grenzen nicht ausrechnen, wenn du die Substitution rückgängig machen willst oder wenn du eine Stammfunktion bestimmen willst
Beispiel 1
∫ x*cos(x2) dx Substitution: u= x2
dx wird durch du ersetzt!
u= x2 ⇒ du/dx = 2x ⇒ dx= du/2x ⇒ xdx= 1/2 du
∫ x*cos(x2)dx = 1/2 ∫ cosu du = 1/2 sin u+ C
Lösung= 1/2* sin(x2)+ C
Info: Bei trigonometrischen Funktionen sollte man die Ableitungen auswendig lernen!!!
Beispiel 2
∫ sin cos2x dx
u=cosx ; u`= -sinx
u=cosx ⇒du/dx= -sinx ⇒ sinxdx= -du
∫sinx cos2xdx= -∫u2 du = -u3/3 +C
Lösung: -1/3 cos3x +C
