Symmetrie und Spiegelung in der Geometrie
In der Geometrie gibt es oft symmetrische Körper. Wenn man diese Symmetrien erkennt, ist dies oft vorteilhaft, weil man dann viele Rechnungen vereinfachen kann.
Symmetrisch ist ein Körper immer dann, wenn man eine Spiegelachse (oder Symmetrieachse) einzeichnen kann. An dieser Achse wird der Körper gespiegelt. Man kann sich die Achse also tatsächlich wie ein Spiegel vorstellen, an der der Körper oder die Zeichnung gespiegelt wird.
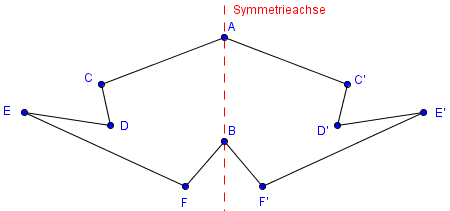
Bei dieser Zeichnung ist alles an der Symmetrieachse die hier in Rot eingezeichnet ist gespiegelt. C wird dabei zu dem gespiegelten Punkt C‘, D wird zu D‘ und so weiter.
Unser Lernvideo zu : Symmetrie und Spiegelung in der Geometrie
Achsenspiegelung
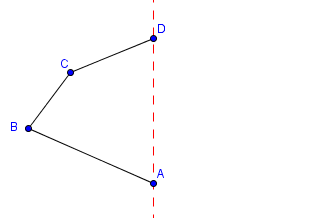
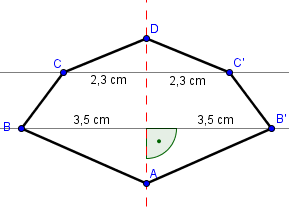
Wir möchten diese Zeichnung an der roten Spiegelachse spiegeln. Dazu müssen wir zunächst die Punkte spiegeln. Die Punkte A und D liegen auf der Spiegelachse und müssen deshalb nicht gespiegelt werden. Wir fangen mit Punkt B an. Wir müssen nun eine Gerade zeichnen die senkrecht zu der Spiegelachse ist und durch den Punkt B geht.
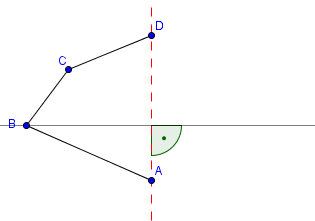
Jetzt müssen wir den Abstand von dem Punkt B bis zu der Spiegelachse entlang der gezeichneten Geraden mit dem Lineal ausmessen. In dem gleichen Abstand Zeichnen wir dann auf der anderen Seite der Spiegelachse den Punkt B‘. Dieser liegt somit auch auf der gezeichneten Geraden.
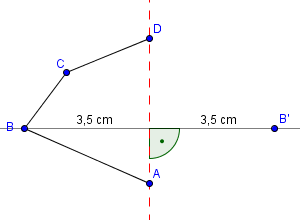
Bei Punkt C gehen wir genauso vor. Auch hier müssen wir wieder eine Senkrechte zu der Symmetrieachse zeichnen, die durch den Punkt C geht und dann im gleichen Abstand auf der gegenüberliegenden Seite den Punkt C‘ einzeichnen. Nachdem wir die Punkte verbunden haben, sieht das Resultat folgendermaßen aus:
Punktspiegelung
Genauso wie man etwas an einer Achse spiegeln kann, kann man es auch an einem Punkt spiegeln. Den Punkt an dem man Spiegelt nennt man Zentrum oder Spiegelzentrum und bezeichnet ihn üblicherweise mit Z. Man geht auch hierbei Punkt für Punkt vor. Die gespiegelten Punkte haben dabei immer den gleichen Abstand zu dem Spiegelpunkt wie der ursprüngliche Punkt. Der ursprüngliche Punkt, der Spiegelpunkt und der gespiegelte Punkt liegen außerdem immer auf einer Linie.
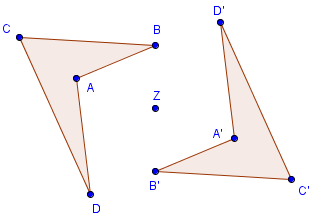
Einen Körper an einem Punkt spiegeln
Wir wollen folgenden Körper an dem Punkt Z spiegeln:
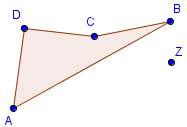
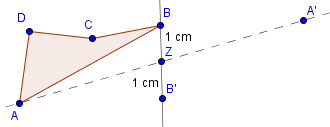
Wir beginnen mit dem Punkt A. Wir Zeichnen eine Gerade durch den Punkt A und Z. Anschließend messen wir den Abstand zwischen A und Z entlang der Geraden. Als letztes zeichnen wir im gleichen Abstand auf der anderen Seite von Z den Punkt A‘ ein, sodass der Abstand zwischen A und Z genauso groß ist wie der Abstand zwischen Z und A‘.
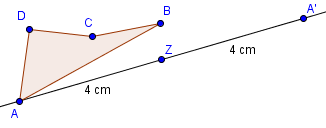
Genauso gehen wir auch bei Punkt B vor. Wir zeichnen eine Gerade durch B und Z und anschließend zeichnen wir im gleichen Abstand den Punkt B‘ ein.
Jetzt fehlen nur noch die Punkte C und D. Wenn man diese auf die gleiche Art und Weise einzeichnet und anschließend die Punkte A bis D verbindet, bekommt man dieses Ergebnis:
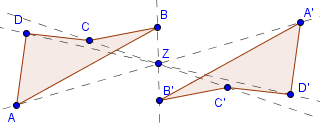
Durch die Punktspiegelung wurde die Figur also um 180° gedreht und natürlich auch verschoben.
Mehrere Spiegelachsen
Man kann eine Figur auch an mehreren Achsen spiegeln. Hierzu ein Beispiel:
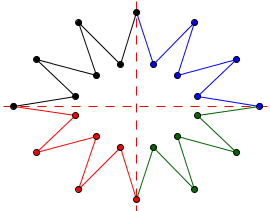
In diesem Beispiel gibt es eine waagerechte und eine senkrechte Spiegelachse. Die Figur oben links wurde zunächst an der waagerechten Achse nach rechts (blau) und unten (rot) gespiegelt. Anschließend wurde die Ausgangsfigur durch eine Punktspiegelung nach unten rechts (grün) gespiegelt. Den grünen Abschnitt hätte man auch durch eine Achsenspiegelung des blauen Abschnitts an der waagerechten Achse oder durch die Achsenspiegelung des roten Abschnitts an der senkrechten Achse erhalten können.
