Wendepunkt berechnen
Wendepunkte
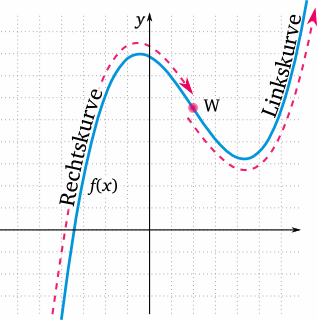
- Wendepunkte sind besondere Punkte einer Kurve: Sie markieren eine Trendwende. Eine Funktion, die vorher fallend war, ist nach dem Wendepunkt steigend während eine Funktion die vorher steigend war, nach dem Wendepunkt fallend ist.
- Ein Wendepunkt ist ein Punkt in einer Kurve, wo sich die Richtung der Kurve ändert. Das heißt wenn die Kurve vorher nach rechts gekrümmt war, krümmt sich die Kurve hinterher nach links. Einen solchen Punkt gibt es auch bei vielen Funktionen. Dieser Punkt ist dort, wo die Steigung der Funktion (Steigung einer Funktion wird durch die Ableitungsfunktion bestimmt) am stärksten ist. Denn vorher wird die Steigung immer stärker und hinterher wieder schwächer durch die entgegengesetzte Krümmung.
- Folglich ist dort, wo die Ableitungsfunktion am extremsten ist (also wo sie einen Extrempunkt hat), ein Wendepunkt vorhanden. Die Extremwerte für eine Funktion berechnete man durch ihre Ableitung, die der Ableitung also durch die zweite Ableitung der Funktion, mit der notwendigen Bedingung, dass diese Null wird.
Unser Lernvideo zu : Wendepunkt berechnen
Beispiel
Unsere Funktion lautet
![]()
Im ersten Schritt bilden wir die ersten drei Ableitungen
![]()
![]()
![]()
Nun kommt das notwendige Kriterium zum Einsatz ![]()
![]()
![]()
Nun kommt das notwendige Kriterium zum Einsatz ![]()
![]() Demnach handelt es sich bei
Demnach handelt es sich bei ![]() um einen Wendepunkt. Wir berechnen den zugehörigen y-Wert indem wir
um einen Wendepunkt. Wir berechnen den zugehörigen y-Wert indem wir ![]() in f(x) einsetzen.
in f(x) einsetzen.
![]()
Der Wendepunkt lautet demnach ![]()
Merke Dir
- Zweite Ableitung berechnen
- Nullstellen der zweiten Ableitung berechnen
- Dritte Ableitung berechnen
- Die in Schritt 2 berechneten x-Werte in die dritte Ableitung ein
-> ist die dritte Ableitung dann ungleich Null, handelt es sich um einen Wendepunkt - Die berechneten x-Werte in die Funktion f(x) einsetzen, um die y-Koordinaten der Wendepunkte zu berechnen
