Dreisatz
Der Dreisatz ist ein mathematisches Verfahren um bei drei gegebenen Werten, die in einem Verhältnis zu einander stehen den Vierten unbekannten Wert zu ermitteln. Oft benötigt wird der Dreisatz bei proportionalen Zuordnungen. Es gibt auch noch den umgekehrten Dreisatz, welchen wir am Ende erläutern.
Lerntool zu Dreisatz
Lösen eines Dreisatzes
Bei einem Dreisatz sind immer drei Werte gegeben. Zwei davon gehören zu einer Menge, der dritte gehört zu einer anderen. Wir möchten nun den unbekannten vierten Wert berechnen. Hierfür benötigen wir beim Dreisatz 2 Schritte. Allgemein geschrieben sieht der Dreisatz folgendermaßen aus:
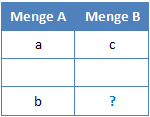
Um den gefragten Wert zu berechnen, berechnen wir zunächst wieviel eine Einheit der Menge A in der Menge B entspricht. Hierfür teilen wir die beiden ersten Werte durch a. Anschließend multiplizieren wir die erhaltenen Werte mit b um den gefragten Wert zu ermitteln:
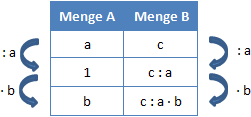
Dieses Vorgehen kann man sich einfach merken und immer danach vorgehen. Man muss nur die Tabelle erstellen, zwischen die beiden bekannten Zahlen eine 1 schreiben und dann erst durch a teilen und anschließend mit b multiplizieren. Wichtig ist dabei, dass man auf beiden Seiten immer dieselbe Operation durchführt. Wenn man zum Beispiel links durch a teilt, muss man rechts auch durch a teilen.
Beispiel 1 – Dreisatzrechnung
Eine Ferienwohnung kostet für 5 Übernachtungen 400€. Wieviel kostet dieselbe Wohnung wenn man 7 Tage übernachten möchte?
Diese proportionale Zuordnung kann man mit Hilfe des Dreisatzes lösen. Dazu sollte man sich zunächst überlegen, welche Werte und Mengen gegeben sind. Hier sind einmal die Anzahl der Nächte und die Kosten gegeben. Wir haben in einer Spalte die Anzahl der Nächte und in der anderen Spalte die Kosten. Da wir zwei Werte für die Anzahl der Nächte haben und nur einen für die Kosten, schreiben wir die Anzahl der Nächte links in die Tabelle. Natürlich könnten wir es auch andersrum aufschreiben.
Es ist jedoch etwas einfacher wenn man immer gleich vorgeht, da dann auch die Rechenschritte sehr einfach zu sehen sind.
Die Tabelle sieht also folgendermaßen aus:
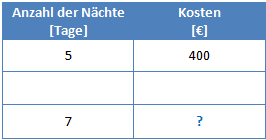
Am besten schreibt man die Einheiten mit in die Titelzeile der Tabelle. Üblicherweise werden diese in eckigen Klammern geschrieben.
Als Erstes schreiben wir nun auf die linke Seite in die Mitte die 1. Hier möchten wir zunächst berechnen wie viel eine Nacht kostet. Wenn wir das wissen, ist es relativ einfach auszurechnen, wieviel 7 Tage kosten werden. Wir schreiben also die 1 auf und berechnen den Wert für eine Nacht indem wir die Kosten von 400 € durch die 5 Tage teilen.
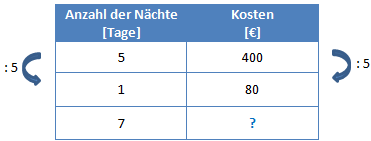
Wir wissen nun also, dass eine Nacht 80€ kostet. Um nun zu berechnen wieviel 7 Nächte kosten, nehmen wir auf beiden Seiten mal 7.

Die Lösung ist also, dass 7 Übernachtungen in der Ferienwohnung 560€ kosten.
Beispiel 2 – Dreisatzrechnung
Für den Bau eines Regals benötigt ein Tischler 2 Stunden. Er nimmt für die Arbeitszeit 60€. Wie lange hätte er für 270€ gearbeitet?
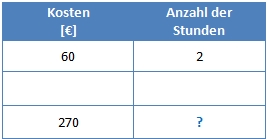
Hier haben wir die beiden Mengen Stunden und Kosten. Bei den Kosten haben wir zwei Werte, deshalb schreiben wir diese in die linke Spalte.
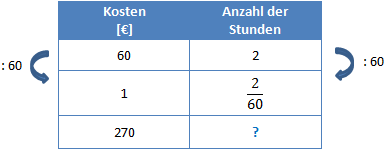
Der nächste Schritt ist wieder zu berechnen, wie lange er für ein Euro gearbeitet hätte. Wir notieren also links in der Mitte die 1 und Teilen durch 60. Wir müssen das Ergebnis nicht als Dezimalzahl schreiben, wir können es als Bruch stehen lassen.
Nachdem wir nun wissen wie lange der Tischler für einen Euro arbeitet, können wir leicht berechnen wie lange er für 270 Euro arbeitet. Wir multiplizieren den Wert einfach mit 270.
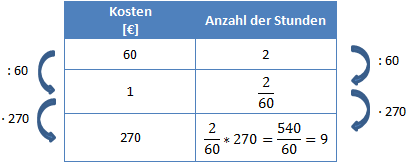
Der Tischler arbeitet für 270€ also genau 9 Stunden.
Hier sieht man relativ gut, dass wir auch direkt die Formel anwenden hätten können, welche am Anfang erwähnt wurde: c : a • b. In diesem Beispiel wäre dies 2 : 60 • 270 = 9. Dadurch spart man sich natürlich ein wenig Arbeit, muss das Ganze aber auch schon relativ gut verstanden haben. Am Anfang ist es auf jeden Fall einfacher sich den Zwischenschritt zu notieren.
Weitere Informationen zum Dreisatz!
