Antiproportionale Zuordnung
Bei der antiproportionalen Zuordnung gibt es zwei Grundsätze. Diese erinnern an die proportionale Zuordnung, sind jedoch genau andersherum.
- Je mehr A, desto weniger B
- Bei einer Verdoppelung von A halbiert sich B
Auch hier sind beide Größen also voneinander abhängig, sie verhalten sich aber ganz anders als bei der proportionalen Zuordnung. Die allgemeine Formel lautet hier:
![]()
k ist hier der Antiproportionalitätsfaktor. Dieser gibt den Zusammenhang zwischen zwei Größen an, welche antiproportional zueinander sind. Um mit antiproportionalen Zusammenhängen rechnen zu können ist der umgekehrte Dreisatz sehr hilfreich der in dem Kapitel „Dreisatz“ beschrieben wird.
Unser Lernvideo zu : Antiproportionale Zuordnung
Beispiel: Antiproportionale Zuordnung
Angenommen ein Handwerker braucht für seine Arbeit 8 Stunden. Wenn er nun nicht alleine wäre, sondern zwei Handwerker an der gleichen Aufgabe arbeiten würden, würden sie natürlich doppelt so schnell sein. Sie würden also nur 4 Stunden brauchen. Es gilt also: Doppelt so viel Handwerker, halb so viel Zeit. Diese Zuordnung ist also antiproportional. Die Antiproportionalitätskonstante erhalten wir indem wir beide Werte miteinander multiplizieren. Dabei ist es egal welche Wertepaare wir nehmen:
1 • 8 = 8 Ein Handwerker braucht acht Stunden.
2 • 4 = 8 Zwei Handwerker brauchen vier Stunden.
Die Antiproportionalitätskonstante ist also 8.
Grafische Darstellung: Antiproportionale Zuordnung
Dieses Beispiel können wir grafisch darstellen. Hierfür benötigen wir eine Wertetabelle. Wir legen die Anzahl der Handwerker fest und rechnen mit folgender Formel die benötigte Zeit aus:
![]()
Für k haben wir in diesem Fall die berechnete 8 eingesetzt.
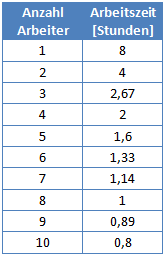
Mit Hilfe der Wertetabelle können wir dann das Diagramm zeichnen. Der Verlauf der antiproportionalen Zuordnung ist dabei typisch. Man nennt diese Art von Kurve auch Hyperbel.
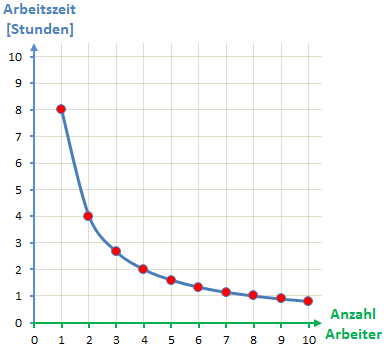
Um die Eigenschaften der Hyperbel noch besser zu erkennen betrachten wir folgendes Diagramm einer antiproportionalen Zuordnung:
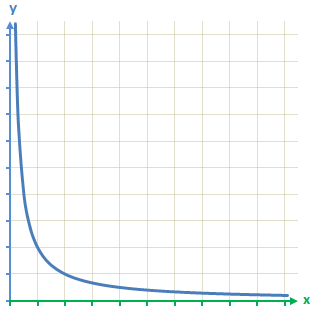
Bei diesem allgemeinen Diagramm sieht man gut, dass der Graph sich oben immer weiter an die y-Achse anschmiegt, sie aber nie ganz erreicht. (0 Arbeiter benötigen theoretisch unendlich viel Zeit) Genauso ist es bei der x-Achse. Auch hier nähert sich der Graph rechts immer weiter an, erreicht sie aber nie.
Sehr viele Arbeiter würden (theoretisch) sehr wenig Zeit brauchen. Sie benötigen aber natürlich immer noch mehr Zeit als 0. Deshalb nähert sich der Graph zwar immer weiter an die x-Achse an, erreicht diese aber nie.
Interessante Fragen und Antworten zu Antiproportionale Zuordnung
Was ist eine antiproportionale Zuordnung? |
| Bei einer Zuordnung wird einem Wert ein anderer Wert eindeutig zugeordnet. Um eine solche Zuordnung zu beschreiben wird folgendes Zeichen benutzt: |—>x |—> y
x wird also y eindeutig zugeordnet. x wird hierbei als Ausgangswert bezeichnet. y gibt den zugeordneten Wert wieder. Ein Beispiel: Wenn ein Gärtner beim Mähen einer vorgegebenen Rasenfläche 12 Minuten braucht und zwei Gärtner für die gleiche Rasenfläche sechs Minuten brauchen, so lässt sich die Zahl der Gärtner der benötigten Arbeitszeit zuordnen. Anzahl Gärtner |—> Arbeitszeit Hieraus ergibt sich folgende Liste: Arbeiter Minuten An dieser Liste erkennen wir, dass sich der linke Wert vergrößert, während sich der rechte Wert verkleinert. Die Entwicklung der beiden Werte verläuft hierbei ganz eindeutig gegenläufig. Wenn also der linke Wert verdoppelt wird, dann wird der rechte Wert halbiert. Wird der linke Wert etwa verdreifacht, so drittelt dich der rechte Wert. Das gegenläufige Wachstum, welches hierbei beobachtet wird, bezeichnen wir als antiproportionale Zuordnung. |
