Drachenviereck
Ein Drachenviereck ist ein ebenes Viereck in dem eine der Diagonalen durch die andere halbiert wird.
•Es ist symmetrisch zu einer Diagonalen
•Diagonalen stehen senkrecht aufeinander
•ein Paar gegenüberliegende Winkel sind gleich groß
•zwei (Paar) gleich lange benachbarte Seiten
•In einem konvexen Deltoiden gilt außerdem, dass auch ein Inkreis existiert, der jede der vier Seiten des Drachenvierecks in genau einem Punkt berührt. Also ist ein konvexer Deltoid ein Tangentenviereck.
Unterschied Drachenviereck und Raute
Drachenviereck
♦eine Symmetrieachse (eine der beiden Diagonalen)
♦zwei Paare gleich langer Seiten – ein Paar gleich großer Winkel
Raute
♦zwei Symmetrieachsen (die beiden Diagonalen)
♦punktsymmetrisch zum Diagonalenschnittpunkt
♦ vier gleich lange Seiten
♦Diagonalen stehen senkrecht aufeinander
♦gegenüberliegende Seiten sind parallel zueinander
♦gegenüberliegende Winkel sind gleich groß → Die Raute ist ein besonderes Drachenviereck bzw. ein besonderes Parallelogramm
Formeln
Bezeichnungen
A = Flächeninhalt
U = Umfang
a, b = Seitenlängen
e, f = Diagonalen
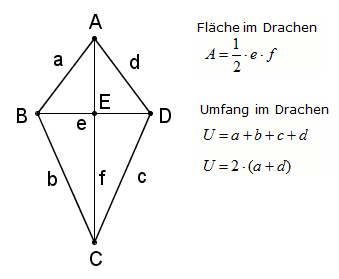
Formel für den Flächeninhalt: Flächeninhalt A = 1/2 *e*f
Formel für den Umfang: U = 2 · a + 2 · b oder U = 2 · (a + b)
Diagonalenlängen und Winkel: lassen sich am besten errechnen indem man durch einzeichnen der Diagonalen das Drachenviereck in Dreiecke zerlegt
a = (U : 2) – b
b = (U : 2) – a
e = A · 2 : f
f = A · 2 : e
