Beweis des Satz des Thales
Den Beweis des Thalessatzes kann man auf zwei verschiedene Arten angehen. Zum einen mathematisch und zum anderen grafisch. Es gibt zwei Vorraussetzungen, die man dafür beachten muss. Beide kennen wir bereits oder ihr könnt gerne nochmal in die vorherigen Themen hineinschnuppern.
Vorraussetzungen
1. Die Winkelsumme eines Dreiecks beträgt immer 180°
2. In einem gleichschenkligem Dreieck sind die Basiswinkel gleich groß
Beide Vorraussetzungen sind Dinge, die wir schon zuvor besprochen haben und somit als gegeben gesehen werden können.
Unser Lernvideo zu : Beweis des Satz des Thales
Mathematischer Beweis
Gegeben ist ein Ursprungsdreieck ABC. Dieses wird in zwei gleichschenklige Dreiecke unterteilt, und zwar vom Mittelpunkt AB bis C. So wird auch der Winkel γ in C geteilt. Nun haben wir zwei gleichschenklige Dreiecke. Eines mit den Punkten CAM und das andere mit den Punkten BCM. Die Basis der Dreiecke sind CA und BC. Die Winkel an der Basis sind gleich groß, das heißt γ =α+β
Wir wissen: γ+α+β = 180°
Einsetzen: α+β+α+β = 180°
Distributivgesetz: 2(α+β) = 180°
Teilen durch 2: α+β = 90°
Somit gilt: γ =α+β = 90°
Hermit ist rechnerisch bewiesen, dass der Winkel γ auf dem Halbkreis immer 90° entspricht.
Grafischer Beweis
Zunächst Zeichnen wir ein Ursprungsdreieck und einen Halbkreis um die längste Seite des Dreiecks.
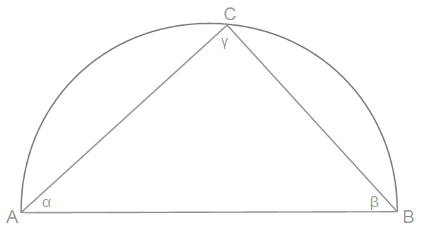
Nun haben wir ein Dreieck mit den Seiten ABC und den dazugehörigen Winkeln.
Als nächstes zeichnen wir eine Seitenhalbierende durch die Seite c.
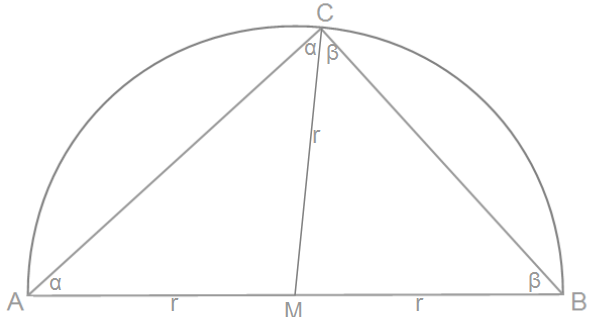
Wir sehen nun unser Ursprungsdreieck unterteilt in zwei kleinere Dreiecke. M ist der Mittelpunkt der Seite c und somit auch der Mittelpunkt des Kreises. Jeder Punkt auf dem Halbkreis vom Mittelpunkt aus entpricht dem Radius r. Somit haben wir nun zwei gleichschenlige Dreiecke in unserem Ursprungsdreieck.
Das erste Dreieck mit den Eckpunkten CAM hat die Basis CA und die Winkel der Basis sind gleich groß. Somit sind beide Winkel so groß wie α aus dem Ursprungsdreieck.
Das zweite Dreieck mit den Eckpunkten BCM hat die Basis BC und die Winkel der Basis sind gleich groß. somit sind beide Winkel so groß wie β aus dem Ursprungsdreieck.
Der Winkel γ wurde von der Seitenhalbierenden geteilt und ist nun die Summe aus α + β.
Wir wissen das die Winkelsumme im Dreieck 180° beträgt, somit auch im Ursprungsdreieck.
Es gilt: γ + α + β = 180° . Da γ = α + β, können wir dieses einsetzen und erhalten:
α + β + α + β = 180° |Distributivgesetz
2(α + β) = 180° | :2
α + β = 90°
Daraus folgt, dass γ = α + β = 90°, also γ = 90°
Somit sit beweisen, dass Punkte auf dem Halbkreis einen Winkel von 90° besitzen.
