Abstand paralleler Geraden
♦Unter dem Abstand zweier paralleler Geraden versteht man die Länge der Verbindungsstrecken der beiden Geraden, die zu den beiden Geraden orthogonal sind.
♦Diese orthogonalen Verbindungsstrecken sind alle gleich lang und gleichzeitig die kürzesten von allen möglichen Verbindungsstrecken der beiden Geraden.
♦Sind z.B. g und h die beiden parallelen Geraden, so benennt man den Abstand der beiden Geraden mit d(g;h) („d“ steht für Abstand)
♦Vom Abstand zweier Geraden kann man eigentlich nur dann sprechen, wenn sich die beiden Geraden nicht schneiden. Dies ist aber nur dann der Fall, wenn die beiden Geraden parallel sind.
Lagebeziehung zwischen den Geraden
Zwei Geraden können verschiedene Lagen zueinander haben:
- Zwei Geraden liegen aufeinander
- Beide Geraden sind zueinander parallel
- Die beiden Geraden schneiden sich in einem Punkt
- Die beiden Geraden sind windschief ( verlaufen weder parallel noch schneiden sich )
- Parallele Geraden haben keinen Schnittpunkt. Der Abstand zweier paralleler Geraden ist überall gleich, denn parallele Geraden haben dieselbe Steigung.
- Zueinander senkrechte Geraden schneiden sich einem Winkel von 90 ° . Sind die Geraden g und h senkrecht zueinander, dann gilt für die Steigungen m g und m h : m g = – 1 m h
Formel
![]()
Beispiel
Wir haben folgende Punkte und Vektoren gegeben und wollen nun den Abstand berechnen. Gegeben haben wir folgendes:
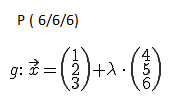
Aus Punkt P und r ( r ist unser λ. Wir haben es nur anders benannt) kann nun eine Ebene gebildet werden. Dazu wird r als der Normalenvektor verwendet und die Ebene in Normalenform geschrieben.Direkt dadrunter steht die Ebene in Koordinatenform (einfach ausmultipliziert mit Skalarprodukt).
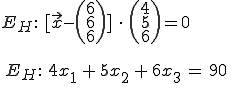
Wir wollen nun den Schnittpunkt zwischen der Geraden und der Hilfsebene berechnen. Dazu setzen wir die Geradengleichung bei der Hilfsebene ein
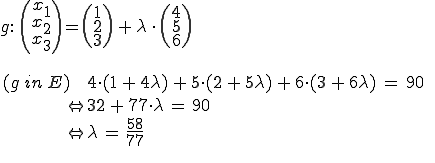
den Wert setzen wir nun in die Geradengleichung ein
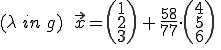
folgt → 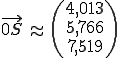
Nun bilden wir den Vektor zwischen dem Schnittpunkt und dem gegebenen Punkt.
Die Länge dieses Vektors ist der Abstand zwischen Punkt und Gerade
![]()
Der Abstand beträt also 2,512 Längeneinheiten!
