Binomialkoeffizient
Binomialkoefffizient:
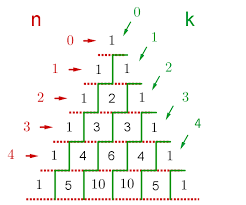
- Der Binomialkoeffizient findet vor allem Anwendung in der Stochastik aber auch in anderen Gebieten der Mathematik. Der Name entstammt der Tatsache, dass man mit Hilfe des Binomialkoeffizienten die Koeffizienten einer Binomialerweiterung einfach bestimmen kann. Der Binomialkoeffizient lässt sich auch durch das Pascalsche Dreieck errechnen.
Notiz: Pascalsche Dreieck
Die Formel für den Binomialkoeffizient lautet
(Wird als „n über k“ oder „k aus n“ gesprochen)
Andere Schreibweisen, wie sie häufig auch auf Taschenrechnern zu finden sind: ,
,
,
und
(Das C steht hierbei für „combinations“ [Kombinationen] oder auch „choices“ [Auswahlmöglichkeiten])
n! ist die Fakultät von n.
Beispiel
Angenommen, du möchtest aus einer Gruppe von n Menschen eine kleinere Gruppe mit k Menschen zusammenstellen, zum Beispiel aus den 30 (=n) Schülern einer Klasse eine Fußballmannschaft von 11 (=k) Spielern.
Dann gibt der Binomialkoeffizient ![]() an, wie wiele verschiedene Fußballmannschaften du bilden kannst.
an, wie wiele verschiedene Fußballmannschaften du bilden kannst.
Ein bisschen formaler: Ich nummeriere die Schüler der Einfachheit halber mit ![]() . Dann wäre eine mögliche Fußballmannschaft:
. Dann wäre eine mögliche Fußballmannschaft:
1. Möglichkeit: ![]()
2. Möglichkeit: ![]()
3. Möglichkeit: ![]()
![]()
![]() . Möglichkeit:
. Möglichkeit: ![]()
Diese Liste von Fußballmannschaften ist also ![]() Fußballmannschaften lang.
Fußballmannschaften lang.
Berechnung mit der Formel ergibt:
Dabei bedeutet ![]() die Fakultät von n, genauer:
die Fakultät von n, genauer: ![]() . Zum Beispiel ist
. Zum Beispiel ist ![]() .
.
Für das Beispiel oben würdest du also rechnen:
(kürzen!)
Unser Lernvideo zu : Binomialkoeffizient
Beispiel 2
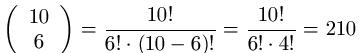
oder
Beispiel 3
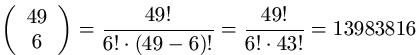
usw….

