Binomialverteilung
Was ist die Binominalverteilung?
- Die Binomialverteilung beschreibt den wahrscheinlichen Ausgang einer Ergebnisfolge eines gleichartigen Versuchs, bei dem nur zwei Ergebnisse möglich sind. Sie zählt zu den bekanntesten Verteilungen der Statistik. Binomialverteilungen sind das Ergebnis von Bernoulli-Experimenten
Vorraussetzung für die Verwendung der Binomialverteilung ist, dass
- a) das Experiment aus gleichen und von einander unabhängigen Versuchen besteht und
- b) die Versuche entweder als Ergebnis „Erfolg“ oder „Misserfolg“ haben dürfen.
Formel für Binominalverteilung
Um die Formel zu verstehen, müssen wir zuerst verstehen, was wir mit ihr erhalten wollen.
Die Erfolgswahrscheinlichkeit der zwei möglichen Ergebnisse einer Ziehung wird wie folgt definiert:
P(Erfolg) = p
P(Misserfolg) = 1 – p
Wenn wir diese bestimmte Serie von Ergebnisse möchten: Erfolg, Misserfolg, Misserfolg, Erfolg
dann können wir auf Grundlage der Definition oben, die Wahrscheinlichkeit, dass wir genau diese Kombination und Reihenfolge von Ergebnisse erhalten, berechnen:
Eine Generelle Formel für Berechnung der Wahrscheinlichkeit, dass man in n Ziehungen eine bestimmte Reihenfolge von Ergebnisse mit r Erfolge erhielt, ist wie folgt:
Da n = Anzahl der Versuche und r = Anzahl der Erfolge muss n – r die Anzahl der Misserfolge sein.
Diese Formel gilt nur für eine Kombination der Ergebnisse.
Jetzt machen wir n Ziehungen, von denen r Ergebnisse “Erfolg“ sein müssen. Die Reihenfolge der Ergebnisse ist egal.
Hier muss man die Kombinatorik-Formel für Ziehung ohne Zurücklegen ohne Beachtung der Reihenfolge verwenden:
Vor der Formel wird auch P(X=r) geschrieben. Damit wird es angegeben, dass man mit dieser Formel die Wahrscheinlichkeit, r Erfolge zu erhalten, berechnen will. X heißt die Zufallsvariable, und sie gibt also nur die Zahl der Erfolge an, die man erhalten will.
Der Formel für die Wahrscheinlichkeit, dass man in n Versuchen r Erfolge erhielt, ist dann wie folgt:
Alle Formel auf einem Überblick ( kleine Formelsammlung)
Kumulierte Wahrscheinlichkeit
Manchmal möchte man die Wahrscheinlichkeit, dass man r oder weniger Erfolge erhielt. In diesem Fall muss man alle die Wahrscheinlichkeiten für P(X) addieren, von X = 0 bis X = r.
Formel lautet:
Standardafvigelsen
Die Standardabweichung beschreibt, wie viel die Zufallsvariable im Verhältnis zu ihrem Erwartungswert abweicht. Sie wird als die Quadratwurzel der Varianz definiert:
Varianz
Die Varianz beschreibt, wie viel es erwarten wird, dass die Ergebnisse sich unterscheiden.
Beispiel 1
Ein Jäger trifft sein Ziel mit einer Wahrscheinlichkeit 40%. Mit welcher Wahrscheinlichkeit erzielt er bei zehn Schüssen mehr als sechs Treffer?
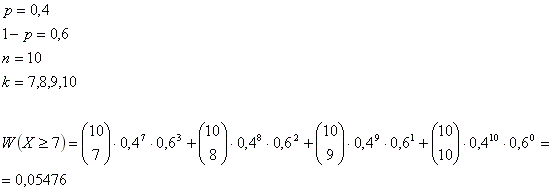
Beispiel 2
Bei einem Automaten gewinnt man in 30% aller Spiele. Wie groß ist die Wahrscheinlichkeit, dass man bei 10 Spielen achtmal gewinnt?
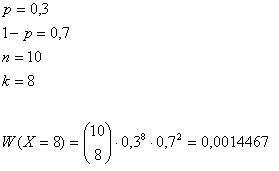
Merkt euch folgendes!
Viele Fragen sich bestimmt die zugrundelegende Idee der Binomialverteilung.
Die Binomialverteilung gibt Wahrscheinlichkeiten für eine bestimmte Anzahl des Auftretens eines Ereignisses bei einem Bernoulliexperiment. Als Bernoulliexperiment wird das mehrmalige Ausführen eines Zufallsversuchs bezeichnet, bei dem es zwei Ergebnisse gibt, die Wahrscheinlichkeit für das Auftreten eines Ergebnisses bei jedem einzelnen Versuchen gleich ist und die einzelnen Versuche voneinander unabhängig sind.
Klassisches Beispiel hierfür ist das mehrmalige Werfen einer Münze. Auch das Würfeln von Sechsern bei einem Würfelspiel wird häufig verwendet.
Ein Würfel kann verschiedene Zahlen anzeigen. Bei vielen Spielen ist es aber besonders vorteilhaft, Sechser zu würfeln. Deshalb könnte die Frage von Interesse sein, wie hoch die Wahrscheinlichkeit ist, bei fünf Würfen drei Sechser zu würfeln. Die Binomialverteilung kann hierauf Antwort geben.
Zunächst zu klären ist, ob ein Bernoulliexperiment vorliegt: Es sind zwei Ereignisse definiert, „Würfeln einer Sechs“ und „Würfeln einer anderen Zahl“. Die Wahrscheinlichkeit eine Sechs zu würfeln, ist immer p = 1/6, die eine andere Zahl als Sechs zu würfeln (1-p) = 5/6. Die Wahrscheinlichkeit ist bei jedem Wurf gleich und die Ergebnisse der Würfe sind unabhängig, schließlich hat der Würfel kein Gedächtnis. Somit liegt ein Bernoulliexperiment vor.
Eine Möglichkeit, bei fünfmaligen Würfeln dreimal eine Sechs zu würfeln. ist, bei den ersten drei Würfen eine Sechs zu würfeln und beim vierten und fünften Wurf eine andere Zahl.
Die Wahrscheinlichkeit, dass das passiert, ist:
![]()
