Exponentialfunktionen
Wir kennen bereits lineare Geichungen (y=mx+c) und auch quadratische Funktionen (f(x)=ax2+bx+c). Bei diesen Gleichungen wird immer nach einer oder mehr Variablen gesucht, die in der Basis stehen.
Suchen wir jedoch nach einer Unbekannten im Exponenten, nennen sich die Gleichungen Exponentialgleichungen oder Exponentailfunktionen.
Exponentialfunktionen haben die Form:
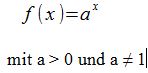
Eine typische Exponentialfunktion sieht folgendermaßen aus:
![]()
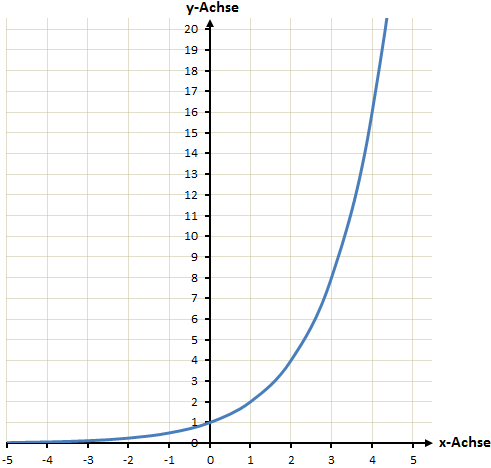
Das Besondere an den einfachen Exponentialfunktionen ist:
- Sie nähern sich im negativen x-Bereich an y = 0 an.
- Sie gehen durch den Punkt P(0/1). (Da
 )
) - Im positiven x-Bereich geht der y-Wert gegen Unendlich.
Wird einer Exponentialfungktion ein Faktor c multipliziert (c darf nicht Null sein), dann hat die Funktionsgleichung die Form: f(x)= c * ax und heißt erweiterte Exponentialfunktion.
Beispiel:
f(x)= 4 * 3x
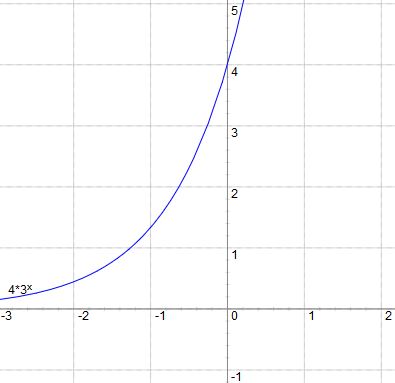
Auch dieser Graph hat bestimmte Eigenschaften:
- Er nähert sich im negativen x-Bereich an y = 0 an.
- Er geht durch den Punkt P(0/4).
- Im positiven x-Bereich geht der y-Wert gegen Unendlich.
Um eine Exponentialgleichung der Form 3 = 2x lösen zu können, benötigen wir den Logarithmus.
Dieser ist im nächsten Artikel erklärt.
Unser Lernvideo zu : Exponentialfunktionen
