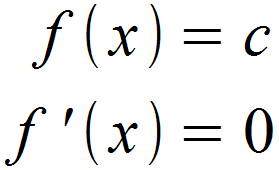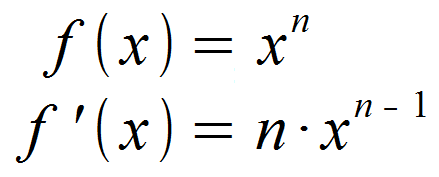Potenzregel zum Ableiten
Mit der Potenzregel kann man für alle Funktionen der Form f (x) = xn direkt die Ableitung angeben. Der Exponent n ist hierbei eine natürliche Zahl und x die Variable, nach der abgeleitet wird.
Wir identifizieren also zunächst n im Exponenten der Potenz von f (x). Dieses n bildet den Faktor vor der Potenz von f '(x). Daraufhin substrahieren wir 1 von n und erhalten den Exponenten der Potenz unserer Ableitung.
Beispiele
Die folgende Potenzfunktion soll abgeleitet werden.
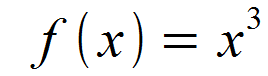
Wir identifizieren n = 3 und setzen dies in die Formel für f '(x) ein.
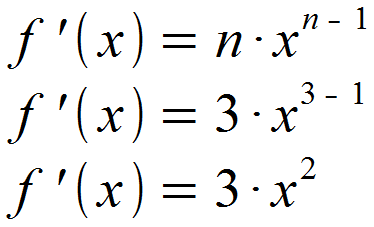
Demnach erhalten wir 3 als Faktor vor der Potenz und 3 - 1 = 2 als Exponenten der Potenz unserer Ableitung.
Unser Lernvideo zu : Potenzregel zum Ableiten
Für die Ableitung von f (x) = x muss die 1 im Exponenten gedacht werden. Setzt man daraufhin n = 1 in die Formel für die Ableitung ein, erhält man 1 als Faktor vor der Potenz und 1 - 1 = 0 als Exponenten. Da jede Potenz mit 0 als Exponent gleich 1 ist, sieht die Ableitung folgendermaßen aus.
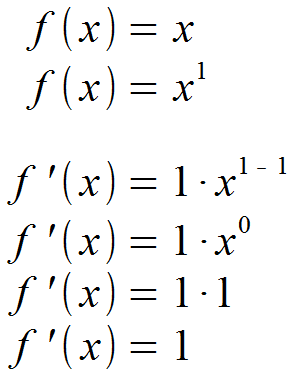
Die Ableitung von f (x) = x ist also f '(x) = 1.

Die Ableitung einer Konstanten, die unabhängig von x ist, beträgt 0.