Stellenwerttafel
Eine Stellenwerttafel nutzen wir um gerade große Zahlen in ihre Bestandteile auf zu bröseln, um sie dann besser bestimmen zu können.
Zum Beispiel die Zahl 1157613 ist auf den ersten Blick schlecht lesbar, nun setzen wir sie in eine Stellenwerttafel
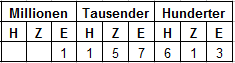
Wir sehen an der Tabelle, dass die Zahl wie folgt gelesen wird:
1 Million, 157 Tausend, 613
Wir betrachten hier das sogenannte Zehnersystem. Dies ergibt sich daraus, dass wir zehn Zahlen haben 0, 1, 2, 3, 4, 5, 6, 7, 8 und 9. Alle anderen Zahlen sind Kompinationen aus diesen zehn.
Zehner- und Zweiersystem
Es gibt in der Mathematik verschiedene Zahlensysteme. Wir wollen uns hier einmal die meist genutzen ansehen. Das ist das Zweiersystem und das Zehnersystem. Das Zehnersystem ist unser ganz normales Zahlensystem und das Zweiersystem wird z.B. für Computersysteme genutzt. Man nennt es auch Binärsystem.
Beispiel 1
Wir betrachten die Zahl 174 im Zehnersystem. Dies wird wie folgt notiert: (174)10
Zur Hilfe nutzen wir die Stellenwerttafel des Zweiersystems. Es beginnt rechts mit den 1er und wird immer dann jeweils verdoppelt
![]()
Hier haben wir zunächst eine Werttafel bis zu den 256ern.
Nun überlegen wir uns für die Zahl 174 wie oft, sie in welche Spalte des Zweiersystems gehört.
Die 256 passt nicht in die 174, daher können wir die Spalte überspringen.
Die 128 passt einmal in die 174. Wir notieren eine 1. Es bleibt: 174 – 128 = 46
Die 64 passt nicht in die 46. Wir notieren eine 0.
Die 32 passt einmal in die 46. Wir notieren eine 1. Es bleibt: 46 – 32 = 14
Die 16 passt nicht in die 14. Wir notieren eine 0.
Die 8 passt einmal in die 14. Wir notieren eine 1. Es bleibt: 14 – 8 = 6
Die 4 passt einmal in die 6. Wir notieren eine 1. Es bleibt: 6 – 4 = 2
Die 2 passt einmal in die 2. Wir notieren eine 1. Es bleibt: 2 – 2 = 0
Daher notieren wir noch eine Null bei den 1ern.
So erhalten wir folgende Zweiertabelle:
![]()
Aus der Tabelle können wir nun entnehmen, dass die Zahl 174 aus dem 10er-System im Zweiersystem die Zahl 10101110 ist.
Beispiel 2
Wir wollen die Zahl (269)10 aus dem Zehnersystem ins Zweiersystem umwandeln.
Wir gehen vor wie oben:
Die Zahl 256 passt einmal in die 269. Wir notieren eine 1. Es bleibt: 269 – 256 = 13
Die Zahl 128 passt nicht in die 13. Wir notieren eine 0.
Die Zahl 64 passt nicht in die 13. Wir notieren eine 0.
Die Zahl 32 passt nicht in die 13. Wir notieren eine 0.
Die Zahl 16 passt nicht in die 13. Wir notieren eine 0.
Die Zahl 8 passt einmal in die 13. Wir notieren eine 1. Es bleibt: 13 – 8 = 5
Die Zahl 4 passt einmal in die 5. Wir notieren eine 1. Es bleibt: 5 – 4 = 1
Die Zahl 2 passt nicht in die 1. Wir notieren eine 0.
Die Zahl 1 passt einmal in die 1. Wir notieren eine 1. Es bleibt: 1 – 1 = 0.
Somit erhalten wir im Zweiersystem die Zahl: 100001101
Das Zweiersystem oder auch Binärsystem ist so wichtig, weil wir es für alle Computerprogramme brauchen. 1 bedeutet nichts anderes als Strom an. 0 bedeutet Strom aus.
Beispiel 3
Nun wollen wir eine Zahl aus dem Zweiersystem ins Zehnersystem umrechnen.
Zur Umrechnung nutzen wir eine Tabelle in die wir die Zahlen übertragen können:
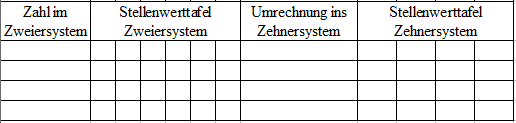
In der Tabelle ist die erste Spalte für die Binärezahl, in der zweiten stehen die Stellenwerte. In der dritten Spalte können wir die Zahl umrechnen und in der vierten Spalte als Zehnersystem eintragen.
Wir betrachten nun die Zahlen: (1101)2, (100111)2 und (11)2. Alle Zahlen stehen im Zweiersystem und sollen ins Zehnersystem gewandelt werden. Wir tragen die binären Zahlen in die erste Spalte. Dann wird in der zweiten spalte die Zahl in die Stellenwerte übertragen. Als nächstes können wir die Stellenwerte zusammenrechnen und als letztes die Zahl ins Zehnersystem übertragen.
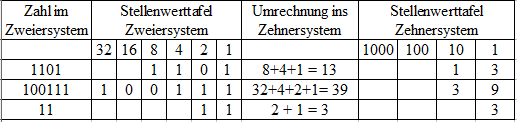
So wird aus der (1101)2 die (13)10. Aus der (100111)2 die (39)10 und aus der (11)2 wird die (3)10.
Somit haben wir die Umrechnungen zwischen Zehner und Zweiersystem kennen gelernt.
Es gibt natürlich noch mehr Stellenwertsysteme, die auf gleiche Weise berechnet werden können.
