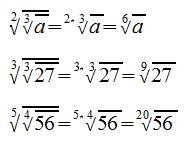Rechnen mit Wurzeln
Mit den eben genannten Regeln kann man Terme umformen und vereinfachen.
Es gilt die allgemeine Aussage:
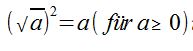
man spricht: Die Wurzel von a zum Quadrat ist gleich a für alle a größer gleich Null.
Die Bedeutung dahinter ist: Wenn man eine positive Zahl a hat, daraus zunächst die Wurzel zieht und dann quadriert erhält man als Ergebnis die Zahl a.
Beispiel 1:
Lerntool zu Rechnen mit Wurzeln
Unser Lernvideo zu : Rechnen mit Wurzeln
Zusammenfassen von Wurzeln
Es gilt:
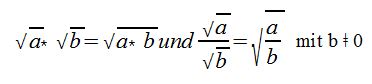
Beispiel 2:
![]()
Hier können wir zwei schwer berechenbare Wurzeln zu einer einfacheren Wurzel zusammenfassen von der wir das Ergebnis einfach berechnen können. Natürlich könnte das Ergebnis theoretisch auch -4 sein!
Beispiel 3
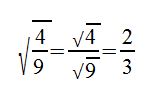
Die Wurzel aus 4/9 zu berechnen scheint auf den ersten Blick relativ schwierig. Dadurch, dass wir aber aus Zähler und Nenner separat die Wurzel ziehen können, wird es deutlich einfacher. Das kann auch -2/-3 sein!
Teilweise Wurzeln ziehen
Wenn man aus einer Zahl a eine Wurzel ziehen mchte, dieses aber nicht ohne weiteres möglich ist, kann man die Zahl auch in Faktoren teilen und dann von einem oder beiden Faktoren die Wurzel ziehen.
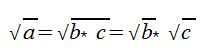
![]()
Hier haben wir die Wurzel in mehrere Faktoren zerlegt, von denen wir einfacher die Wurzel ziehen können. Zwar enthält die Lösung immer noch eine Wurzel, diese ist jedoch deutlich kleiner als die Ursprungswurzel und wir können uns darunter viel mehr vorstellen als vorher.
Wurzeln radizieren
Wurzeln radizieren, bedeutet aus einer Wurzel eine Wurzel ziehen. Dazu gilt folgende allgemeine Aussage:
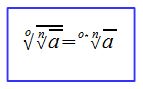
Wir sehen an der allgemeinen Aussage, dass wir bei einer Radizierung einer Wurzel die Wurzelexponenten o und n werden multipliziert. Der Radikant a bleibt dabei unverändert.
Beispiele: