Nullstellen berechnen (quadratische Ergänzung)
Mithilfe der quadratischen Ergänzung können wir die Nullstellen von quadratischen Funktionen berechnen. Das Vorgehen ähnelt dabei dem für die Umrechnung von Normal- zu Scheitelpunktform.
Eine quadratische Funktion kann keine, eine oder zwei Nullstellen besitzen. Mit diesem Verfahren erfahren wir wie viele und welche Nullstellen eine quadratische Funktion hat. Wir beginnen damit, dass wir die Funktion gleich 0 setzen. Wir wollen also die x-Werte für y=0 berechnen.
Beispiel
Wir zeigen das Vorgehen anhand eines Beispiels. Wir beginnen mit einer Funktion in der Normalform und zeigen später den Einstiegspunkt an dem man beginnen muss wenn man eine Funktion in der Scheitelpunkt gegeben hat.
![]()
Zunächst einmal müssen wir dafür sorgen, dass x² ohne Vorfaktor steht. Man nennt diesen Schritt auch „normalisieren“. Wir teilen dafür durch 3:
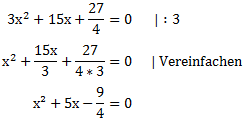
Jetzt nehmen wir die quadratische Ergänzung vor. Diese ist im Kapitel „quadratische Ergänzung“ genauer erklärt.
![]()
Anschließend können wir die binomische Formel anwenden:
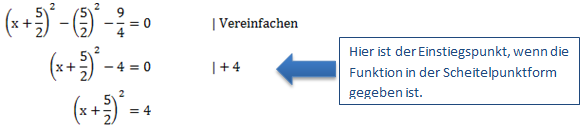
Da das x in der Klammer steht und quadriert wird, müssen wir nun die Wurzel ziehen um an das x heran zu kommen.
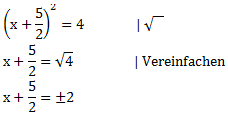
An dieser Stelle müssen wir die Wurzel aus 4 ziehen. Die Wurzel aus 4 ist entweder +2 oder -2. Deshalb müssen wir die Rechnung nun in zwei Pfade aufteilen, um beide Möglichkeiten zu berücksichtigen.
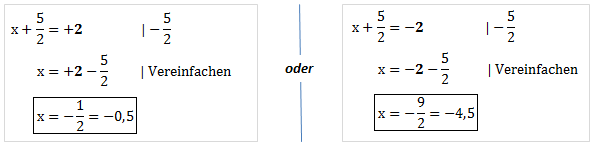
Wir erhalten bei dieser Rechnung zwei Ergebnisse. x kann also entweder -0,5 oder -4,5 sein. Zur Kontrolle setzen wir beide Werte in die Ausgangsgleichung ein und überprüfen das Ergebnis.
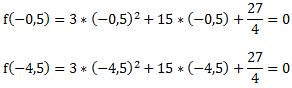
Bei beiden berechneten Werten erhalten wir wie erwartet null als Ergebnis. Die Nullstellen liegen also bei x = -0,5 und x = -4,5.
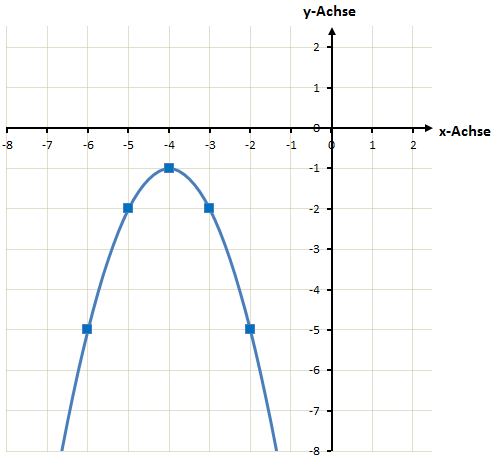
Hier noch einmal die gezeichnete Funktion. Auch hier sehen wir die Nullstellen bei den berechneten Werten.
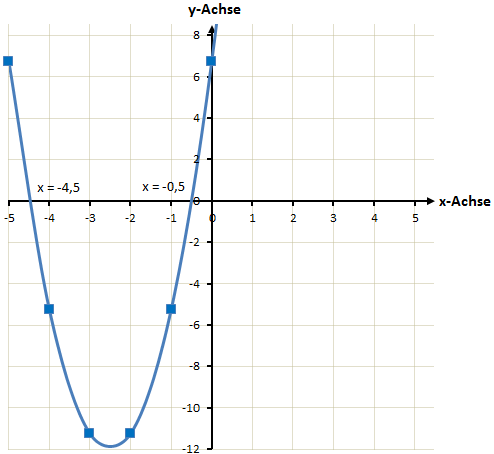
Beispiel: Quadratische Funktion mit nur einer Nullstelle
In dem ersten Beispiel hatte unsere quadratische Funktion genau zwei Nullstellen. Durch die Fallunterscheidung, welche aus dem ziehen der Wurzel resultierte, sind wir auf beide Nullstellen gekommen. Wenn die quadratische Funktion nur eine Nullstelle hat, benötigen wir keine Fallunterscheidung, da sich unter der Wurzel der Wert 0 ergibt. Wir beginnen genau wie bei dem vorhergehenden Beispiel. Wir nehmen folgende Funktion:
![]()
Wir setzen die Gleichung gleich null, normalisieren sie (sodass vorne nur noch x² steht) und wenden dann die quadratische Ergänzung und die binomische Formel an.
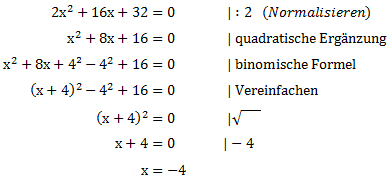
Da die Wurzel von 0 gleich 0 ist, benötigen wir keine Fallunterscheidung und erhalten als einzige Lösung x = -4. Zur Kontrolle setzen wir -4 in die Funktion f(x) ein.
![]()
Hier die gezeichnete Funktion:
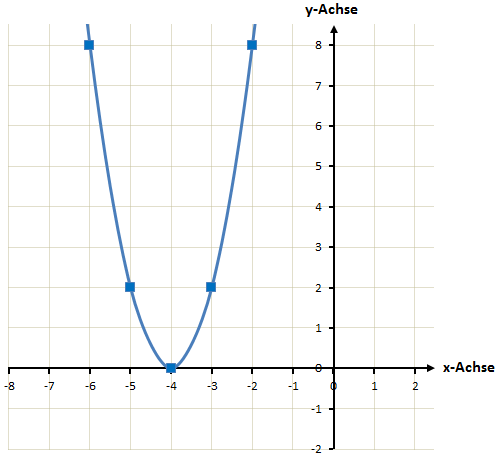
Beispiel: Quadratische Funktion mit keiner Nullstelle
Wenn eine quadratische Funktion keine Nullstellen besitzt und wir diese gleich 0 setzen, erhalten wir keine Lösung. In diesem Fall müssten wir die Wurzel aus einem negativen Wert ziehen. Da die Wurzel für negative Zahlen aber nicht definiert ist, ist die Gleichung dann unlösbar. Die Lösungsmenge ist also leer und die Funktion besitzt keine Nullstellen.

Die Funktion hat dementsprechend keine Nullstellen. Hier noch einmal die gezeichnete Funktion: