Nullstellen berechnen (PQ-Formel)
Eine andere Möglichkeit die Nullstellen zu berechnen ist die PQ-Formel. Diese können wir anwenden, wenn die Funktion in der Normalform gegeben ist. Die PQ-Formel sieht folgendermaßen aus:
![]()
Wir erhalten die beiden Lösungen ![]() und
und ![]() je nachdem ob wir addieren oder subtrahieren. Die Ausgangsgleichung sieht in diesem Fall so aus:
je nachdem ob wir addieren oder subtrahieren. Die Ausgangsgleichung sieht in diesem Fall so aus:
![]()
Wir werden die Gleichung hier nicht im einzelnen herleiten. Wenn man die Gleichung allerdings versucht mit der quadratischen Ergänzung zu lösen und dabei keine Zahlen einsetzt, sondern mit den Variablen rechnet, kommt man automatisch auf die PQ-Formel. Sie ist also kein anderer Weg, sondern fasst den zuvor beschriebenen Weg nur zusammen, sodass man direkt die Lösung erhält. Wir zeigen das Vorgehen hier an demselben Beispiel, welches wir auch für die quadratische Ergänzung benutzt haben.
Unser Lernvideo zu : Nullstellen berechnen (PQ-Formel)
Beispiel
![]()
Vor der Anwendung der PQ-Formel müssen wir die Funktion gleich 0 setzen und normalisieren.

An dieser Gleichung können wir nun unsere Parameter für die PQ-Formel ablesen:
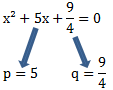
Diese Werte setzen wir nun in die PQ-Formel ein und vereinfachen diese anschließend:
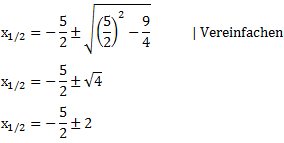
Wir erhalten zwei Lösungen. Eine wenn wir addieren und eine wenn wir subtrahieren.
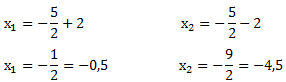
Wir erhalten auf diesem Weg natürlich dieselben Nullstellen, die wir auch mit Hilfe der quadratischen Ergänzung erhalten haben.
Quadratische Funktionen mit einer oder keiner Nullstelle
Ähnlich wie bei der Anwendung der quadratischen Ergänzung und der binomischen Formeln ergibt sich bei einer Funktion mit einer Nullstelle, dass unter der Wurzel der PQ-Formel eine 0 steht. Eine Fallunterscheidung ist damit nicht nötig.
Bei Funktionen ohne Nullstellen erhalten wir eine negative zahl unter der Wurzel der PQ-Formel. Es gibt dementsprechend keine Lösung der Gleichung.
Interessante Fragen und Antworten zu Nullstellen berechnen (PQ-Formel)
Kommt man mit der pq Formel zum selben Ergebnis wie mit der Mitternachtsformel? |
| Zwar unterscheiden sich die Formel der Mitternachtsformel und die der PQ- Formel. Jedoch kommt bei der richtigen Anwendung dieser beiden Formeln, das selbe Endergebnis heraus. Somit gibt es keinen Unterschied bezüglich des Ergebnisses. Jedoch kann es passieren, dass bei einigen Aufgaben die PQ-Formel oder die Mitternachtsformel zu Problemen führen kann. Somit muss bei der PQ-Formel beachtet werden, dass diese immer so umgeformt werden muss, dass der Koeffizient bei x^2 eine 1 ist (a = 1). Diese Vorgehensweise hat daher den Nachteil, dass oft mit Brüchen weiter gerechnet werden muss. Daher können sich kleine Fehler einschleichen. Bei der Mitternachtsformel ist diese Umformung nicht nötig. |
Warum heißt die pq Formel wie sie heißt? |
| Jeder Schüler wird mit ihr in Berührung kommen, wenn es um das Berechnen von Nullstellen geht. Die Rede ist von der pq-Formel. Doch woher hat die Formel ihren doch recht ungewöhnlichen Namen?Die Antwort ist denkbar simpel. Bei der pq-Formel handelt es sich um eine Formel, in der die Werte für p und q noch eingesetzt werden müssen. Diese Werte werden aus der ursprünglichen Gleichung abgelesen, für die die Nullstellen bestimmt werden sollen. Der Rest der Formel ist fix, lediglich p und q variieren von Anwendungsfall zu Anwendungsfall. Da diese beiden Variablen so essenziell für das Berechnen der Nullwerte ist, würde die dazugehörige Formel kurzerhand pq-Formel getauft. |
Was kann man alles mit einer pq Formel lösen? |
| Mit der PQ-Formel können quadratische Gleichungen gelöst werden. Das bedeutet also, dass alle Gleichungen zweiten Grades mithilfe dieser Formel gelöst werden können. Bevor mit der PQ-Formel eine solche Gleichung gelöst werden kann, muss diese zu erst in die Normalform gebracht werden. Jedoch gibt es einige quadratische Gleichungen, die nicht gelöst werden können. Dies sind Gleichungen, die beim Einsetzen in die PQ-Formel eine negative Wurzel aufweisen. Sollte also unter der Wurzel eine negative Zahl stehen, dann hat die Gleichung keine Lösung.Doch es können auch biquadratische Gleichungen mithilfe der PQ-Formel gelöst werden. Jedoch kann die PQ-Formel eine solche Gleichung nicht alleine lösen. Um eine solche Gleichung losen zu können, muss vorher eine Substitution durchgeführt werden. |
Wie löst man eine quadratische Gleichung mit der pq Formel? |
| Zu Beginn gilt es zu klären, was eine quadratische Gleichung ist. Dabei handelt es sich um eine Gleichung mit der Form ax2 + px + q = 0. Jede andere Gleichung lässt sich in diese Form bringen. Um die pq-Formel nutzen zu können, muss a ungleich Null sein.Das grundlegende Vorgehen ist stets das gleiche. Im ersten Schritt muss die Gleichung auf die Form x2 + px + q = 0 gebracht werden. Nun lassen sich auch p und q sehr leicht ablesen. Die jeweiligen Werte werden in die pq-Formel eingetragen und anschließend die Lösung berechnet.
Dies soll an einem einfachen Beispiel gezeigt werden. Gegeben ist die Gleichung x^2 + 4x + 4 = 0. P ist demnach 4, q ist ebenfalls 4. Werden die Werte in die Formel eingetragen und diese aufgelöst, so ergibt sich für den einen x-Wert -2 + 0 = -2 und für den anderen x-Wert -2 -0 = -2. |
