Einführung – Sinus, Kosinus, Tangens
Die Trigonometrie hilft uns bei der Dreiecksberechnung. Mit ihr können wir unbekannte Winkel oder Strecken im rechtwinkligen Dreiecken berechnen. Es gibt dabei drei Basisfunktionen die jeweils das Verhältnis von bestimmten Seiten beschreiben. Zunächst einmal benötigen wir einige Begriffe.
Grundbegriffe
In einem rechtwinkligen Dreieck gibt es immer eine lange Seite und zwei kürzere. Die lange Seite ist die Seite die dem rechten Winkel gegenüber liegt. Sie ist die längste Seite und wird Hypotenuse genannt. Die beiden kürzeren Seiten heißen Katheten. Die Hypotenuse wird mit üblicherweise mit dem Buchstabe c bezeichnet. Die beiden Katheten mit a und b.
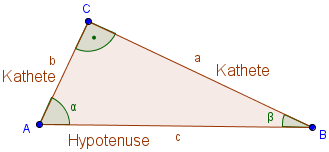
Die Winkel werden wie üblich mit α und β benannt. Der rechte Winkel erhält keine Bezeichnung, da er nicht weiter benötigt wird.
Unser Lernvideo zu : Einführung – Sinus, Kosinus, Tangens
Sinus, Kosinus und Tangens
Sinus, Kosinus und Tangens geben nun unterschiedliche Verhältnisse im Dreieck an:

Welche Seiten damit genau gemeint sind, ist von der Lage des betrachteten Winkels abhängig. Mit der Gegenkathete ist immer die Kathete gemeint die sich gegenüber von dem jeweiligen Winkel befindet. Mit der Ankathete ist die Kathete gemeint die sich an dem Winkel dran befindet.
Die drei Formeln für Sinus, Kosinus und Tangens sollte man sich am besten sehr gut merken. Sie werden in der Trigonometrie ständig benötigt.
Die folgenden Beispiele beziehen sich auf das oben gezeigte Dreieck:
Beispiel Sinus
![]()
Um Sinus α berechnen zu können, müssen wir die Gegenkathete durch die Hypotenuse teilen. Die Gegenkathete ist in diesem Fall a, da sich die Kathete a gegenüber von dem Winkel α befindet.
![]()
Ähnlich wie eben müssen wir wieder den Sinus berechnen. Diesmal allerdings von dem Winkel β. Deshalb ist nun die Gegenkathete eine andere. Die Gegenkathete ist nun b, da sich b Gegenüber dem Winkel β befindet. Die Hypotenuse ist natürlich in allen Fällen dieselbe.
Beispiel Kosinus
![]()
Genau wie beim Sinus müssen wir nun auch bei Kosinus vorgehen. Nur beim Kosinus müssen wir natürlich die Ankathete benutzen. Diese ist b, da b sich am Winkel α befindet.
![]()
Hier müssen wir die Ankathete von β nutzen. Die Ankathete von β ist a. Die Hypotenuse ist wie schon gesagt immer die längste Seite c.
Beispiel Tangens
![]()
Ähnlich verhält es sich beim Tangens. Hier müssen wir die Gegenkathete durch die Ankathete teilen. Beim Winkel α ist dies also a durch b.
![]()
Analog dazu ist der Tangens vom Winkel β b durch a.
Beispiele Sinus, Kosinus, Tangens
Die Bezeichnungen der Winkel und Seiten im Dreieck kann natürlich auch anders sein. Wir müssen also immer aufpassen, welche Seiten durch einander geteilt werden müssen.
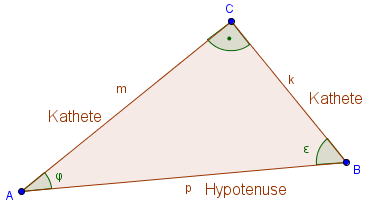
Bestimme:
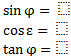
Wir nehmen uns zuerst sin φ vor. Dazu müssen wir den Winkel im Dreieck suchen. Er befindet sich unten links. Sinus ist Gegenkathete geteilt durch Hypotenuse. Die Hypotenuse ist klar, diese ist p, da p die längste Seite ist und dem rechten Winkel gegenüber liegt. Die Gegenkathete ist in diesem Fall k, da k die Kathete ist die φ gegenüber liegt. Es gilt hier also:
![]()
Bei cos ε gehen wir genauso vor. Wir suchen den Winkel ε. Er befindet sich rechts. Für den Kosinus brauchen wir die Ankathete und die Hypotenuse. Die Ankathete ist k, da sie am Winkel ε dran liegt. Die Hypotenuse ist natürlich wieder p. Es ergibt sich:
![]()
Es gilt also:
![]()
Dieser Zusammenhang gilt immer.
Es fehlt nun nur noch tan φ. Hierfür teilen wir die Gegenkathete durch die Ankathete von φ. Die Gegenkathete k haben wir eben schon bei sin φ benutzt. Die Ankathete von φ ist m.
![]()
Interessante Fragen und Antworten zu Einführung – Sinus, Kosinus, Tangens
Was genau rechnet man mit Sinus, Cosinus und Tangens aus? |
Mit Sinus, Cosinus und Tangens lassen sich die Winkel eines rechtwinkligen Dreiecks berechnen. Ein rechtwinkliges Dreieck besitzt, wie der Name schon sagt, einen rechten Winkel. Der Winkel, welcher sich auf der anderen Seite befindet, also links, wenn der rechte Winkel rechts ist und umgekehrt, wird als ? (Alpha) bezeichnet. Gegenüber von diesem Winkel befindet sich die Seite a. Diese wird als Gegenkathete bezeichnet. Direkt am Winkel ? befindet sich die Seite b, die Ankathete. Die Seite c ist die Hypotenuse. Sie ist die längste Seite vom rechtwinkligen Dreieck und befindet sich immer gegenüber dem rechten Winkel.
SinusDer Sinus wird verwendet, wenn die Längen der Gegenkathete und der Hypotenuse bekannt sind. Um nun den Winkel zu berechnen wird die Gegenkathete durch die Hypotenuse geteilt. Besitzt die Gegenkathete (Seite a, gegenüber von ?) beispielsweise eine Länge von 3 cm und die Hypotenuse (Seite c, gegenüber des rechten Winkels) eine Länge von 5 cm, so kann ? berechnet werden, indem: sin ? = 3 cm : 5 cm = 0,6 (Taschenrechner arcsin 0,6 ) = ? 36,87 Grad gerechnet wird. CosinusDer Cosinus wird verwendet, wenn die Längen der Ankathete (Seite b, an ?) und der Hypotenuse (Seite c, gegenüber rechter Winkel) bekannt sind. Hierzu wird die Ankathete durch die Hypotenuse geteilt. Besitzt die Ankathete beispielsweise eine Länge von 3 cm und die Hypotenuse eine Länge von 5 cm, so ergibt sich: cos ? = 3 cm : 5 cm = 0,6 (Taschenrechner arccos 0,6) = ? 53,13 Grad. Tangens Sind die Längen der Ankathete und der Gegenkathete bekannt, so kann über den Tangens der Winkel berechnet werden. Hierzu wird die Gegenkathete (Seite a) durch die Ankathete (Seite b) geteilt. Ist a beispielsweise 3 cm lang und b ebenfalls, so besitzt der Winkel ?: tan ?= 3 cm : 3 cm = 1 (arctan 1) = 45 Grad. |
Was haben Sinus, Cosinus und Tangens mit Winkeln zutun? |
| Sinus, Cosinus und Tangens hängen mit dem spitzen Winkel im rechtwinkligen Dreieck zwischen Hypotenuse und Ankathete zusammen. Deshalb werden sie auch als Winkelfunktionen bezeichnet.Stellen wir uns ein rechtwinkliges Dreieck folgendermaßen vor: Die untere Linie nennt man Hypotenuse. die nach links im Eckpunkt A und nach rechts im Eckpunkt B endet. Über der Hypotenuse befindet sich der Eckpunkt C, der so mit den Punkten A und B verbunden ist, dass die Verbindungslinie zwischen A und C mit der Verbindungslinie zwischen C und B einen rechten Winkel, also einen Winkel von 90 Grad bildet. Die Verbindung von A nach C wird Kathete, oft zum besseren Verständnis auch Ankathete genannt. Sie bildet mit der Hypotenuse den spitzen Winkel, auf den sich Sinus, Cosinus und Tangens beziehen. Er wird häufig mit dem griechischen Buchstaben Alpha bezeichnet. Die Verbindung zwischen den Ecken C und B nennt man Gegenkathete.
In der Mathematik lassen sich konkrete Werte für Winkel und Längen von rechtwinkligen Dreiecken berechnen, wozu man die Winkelfunktionen Sinus, Cosinus und Tangens benutzt. Dabei beschreibt der Sinus des oben genannten Winkels Alpha das Verhältnis von Gegenkathete zu Hypotenuse, anders ausgedrückt: Sinus Alpha ist gleich Länge der Gegenkathete dividiert durch Länge der Hypotenuse. Analog dazu ergibt sich der Cosinus des Winkels Alpha als Quotient Länge der Ankathete dividiert durch Länge der Hypotenuse. Cosinus ist die Komplementärfunktion zum Sinus des betrachteten Winkels. Der Tangens berechnet sich als Verhältnis der Länge der Gegenkathete zur Länge der Ankathete. Man kann auch Sinus Alpha durch Cosinus Alpha dividieren und erhält so den Tangenswert des Winkels Alpha. Der Alpha gegenüber liegende spitze Winkel, meist mit Beta bezeichnet, lässt sich ebenfalls über Sinus, Cosinus oder Tangens im Zusammenhang mit bekannten Seitenlängen berechnen. |
Was unterscheidet Sinus und Cosinus von Tangens? |
| Bei Sinus, Cosinus und Tangens handelt es sich um trigonometrische Funktionen, mit deren Hilfe die Winkel eines Dreieckes berechnet werden können. Zum Berechnen eines Winkels dürfen Sinus-, Kosinus- und Tangens-Funktion nur für ein rechtwinkliges Dreieck genutzt werden. Zudem liegt der Winkel stets zwischen 0° und 90°.Hauptsächlich unterscheiden sich die drei Funktionen in der Art ihrer Berechnung. Während beim Sinus die Gegenkathete durch die Hypotenuse geteilt wird, ist es beim Cosinus die Ankathete und die Hypotenuse, aus denen der Quotient gebildet wird. Beim Tangens wiederum wird die Gegenkathete durch die Ankathete dividiert. Der Tangens ist demnach die einzige Funktion, die nicht mit der Hypotenuse arbeitet. |
Wie berechne ich den Cosinus Alpha wenn ich den Sinus Alpha gegeben habe? |
| Wie schon erwähnt beinhaltet der Sinus von Alpha den Zusammenhang von Gegenkathete zur Hypotenuse und der Cosinus von Alpha wiederum den Zusammenhang von Ankathete zur Hypotenuse. Zusätzlich kann man mit Hilfe des schon bekannten Satz von Pythagoras auf eine weitere Beziehung geschlossen werden, nämlich dem sogenannten Trigonometrischen Pythagoras. Dieser besagt, dass(sin(alpha))^2 + (cos(alpha))^2 = 1
Dies lässt sich am Besten am Einheitskreis verdeutlichen. Zunächst betrachtet man den Satz von Pythagoras: a^2 + b^2 = c^2 Mit dem obigen Zusammenhang von Sinus und Cosinus lässt sich auf folgende Beziehung schließen: sin(alpha) = (Gegenkathete) / (Hypotenuse) Einsetzen liefert: (sin(alpha) * Hypotenuse)^2 + (cos(alpha) * Hypotenuse)^2 = (Hypotenuse)^2 , ausklammern der Hypotenuse aus dem linken Teil der Gleichung: Durch kürzen der Hypotenuse von beiden Seiten der Gleichung erhält man nun schließlich den Zusammenhang: (sin(alpha))^2 + (cos(alpha))^2 = 1 Mit diesem Zusammenhang lässt sich nun die Beziehung zwischen Cosinus und Alpha besser verstehen. Abschließend noch ein Anwendungsbeispiel des Satzes. (sin(alpha))^2 + (cos(alpha))^2 = 1 nach (cos(alpha))^2 umstellen, also Im Beispiel sind sin(alpha) = 0,5, folglich also (sin(alpha))^2 = (0,5)^2 = 0,25 Dies eingesetzt in die Gleichung ergibt: (cos(alpha))^2 = 1 – 0,25 = 0,75 Im letzen Schritt muss dann noch lediglich die Wurzel gezogen werden: cos(alpha) = Wurzel(0,75) = Wurzel(3) / 2 |
Wie findet man aus Tangens den Cosinus und Sinus herausfinden? |
| Bei der Winkelberechnung mit Cosinus, Sinus und Tanges nutzt jeder Satz zwei Angaben, die sich aus Hypotenuse, Gegenkathete und Ankathete zusammensetzen. Das bedeutet, dass jeder Satz immer einen Teil der anderen beiden nutzt. Durch diesen Zusammenhang von Cosinus, Sinus und Tanges erhält man bei der Berechnung des einen immer auch ein Teilergebnis der anderen.Wird der Tanges berechnet, so ist am Ende die Ankathete und die Gegenkathete bekannt. Für Cosinus und Sinus wird zusätzlich die Hypotenuse benötigt. Diese lässt sich ausrechnen, da durch die Berechnung des Tangens nun auch ein Winkel bekannt ist. Angenommen, es handelt sich um den Winkel ?, so sind nun die Seiten b (Ankathete) und a (Gegenkathete) bekannt. Nutzt man jetzt den Sinus oder Cosinus von ?, führen diese Angaben automatisch zur Hypotenuse. Damit sind alle Seitenangaben des Dreiecks bekannt und Sinus und Cosinus können ebenfalls berechnet werden.
Sobald eine Winkelfunktion bekannt ist, lassen sich durch die Abhängigkeit der anderen auch diese ohne große Mühe berechnen. |
Wo liegen bei Sinus und Cosinus eigentlich die Nullstellen und wie findet man diese? |
| In der Schulzeit zählen Sinus, Kosinus und Tangens zu den wichtigsten Inhalten, die wir lernen. Diese drei Funktionen werden im Wesentlichen dazu benötigt, um exakte Berechnungen anstellen zu können. Sie dienen dabei vor allem der Vereinfachung ansonsten komplexer Zusammenhänge.
Was aber ist mit den Nullstellen, wo liegen diese bei Sinus und Cosinus eigentlich und wie kann man sie am besten finden? Zuerst einmal sei erwähnt, dass die Nullstellen bei der Tangens und Sinusfunktion übereinstimmen, nicht jedoch bei der Kosinusfunktion. Dieser Fehler wird nämlich von vielen begangen, die wissen, dass es eine Übereinstimmung gibt, nicht jedoch, wo diese zu finden ist. Zur Berechnung der Nullstellen gibt es mehrere Gleichungen, die je nach Sachverhalt auf die jeweils passende Weise verwendet werden müssen. Sie zu kennen gehört zu den Grundlagen der Mathematik, weswegen dies der erste Schritt zur Feststellung der Nullstellen sein sollte. Was dafür getan werden muss, ist das Einsetzen der richtigen Zahlen, ansonsten kann es nämlich schnell zum einen oder anderen Rechenfehler kommen. Abgehandelt wird das Thema trigonometrische Zahlen zwar vor allem in der Schule, in viele Berufen bleibt es jedoch auch zu einem späteren Zeitpunkt von entscheidender Bedeutung. Die Berechnung der Nullstellen ist also etwas, das jeder möglichst gut beherrschen sollte. |
