Ebener Vektor und räumlicher Vektor
Vektoralgebra
Wir befassen uns mit dem Thema Vektoralgebra. Dabei unterscheiden wir zwischen dem Ebenen Vektor und dem räumlichen Vektor.
Was der Unterschied zwischen beiden ist, werden wir durch ein Beispiel im folgenden veranschaulichen.
Was ist eigentlich ein Ebener Vektor? (2D)
Ein Ebener Vektor ( 2D) wird geometrisch durch Pfeile in der Ebene dargestellt. Im folgenden seht ihr ein Bild. Stellt euch vor der Punkt A ist der Startpunkt am dem ihr los läuft. Geht ihr dabei 1 Meter nach rechts und 2 Meter nach oben, erreicht ihr den Punkt (1;2). Der Pfeil vom Ursprung A bis zum Endpunkt B ist euer neuer Vektor. Neuer Punkt Vektor genannt! Diese schreibt ihr mathematisch folgendermaßen:
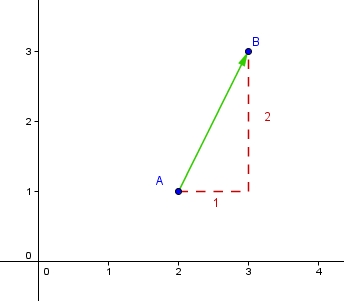
Wir wissen, dass durch die Zeichnung der Punkt A und Punkt B folgende Werte aufweisen!
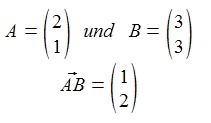
Hierbei besteht folgender Zusammenhang
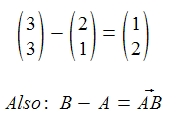
Was bedeutet der Zusammenhang?
Wir berechnen also einen Vektor durch die Formel: Vektor = Endpunkt – Anfangspunkt
Hier könnt ihr folgende Formel benutzen!
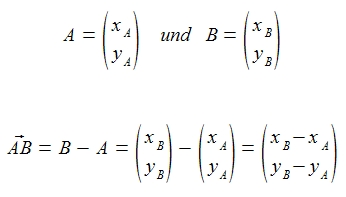
Unser Lernvideo zu : Ebener Vektor und räumlicher Vektor
Was ist ein räumlicher Vektor?
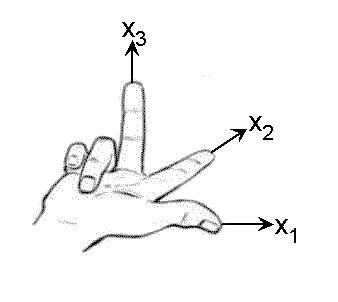
Im Gegensatz zum 2D Vektor (Ebener Vektor) bewegen wir uns nicht nur in der Länge und Breite, sonder auch in der Höhe! Deshalb auch 3D Vektor genannt! Dabei reicht uns nicht mehr ein Koordinatensystem mit x und y. Sondern wir nehmen jetzt eine Richtung dazu. Richtung „z“. Und haben somit ein Koordinatensystem (x;y;z)
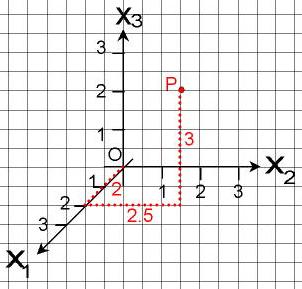
Stellt euch vor, der Punkt x=0 ist euer Startpunkt. Ihr läuft von dort aus 2 Meter in X1-Richtung. Dann wieder 2,5 Meter in X2-Richtung und von dort aus 3 Meter nach oben! Somit hat unsere Koordinaten folgende Punkte
P=(2, 2;5 ,3)
Zur Orientierung im Koordinatensystem könnt ihr euch mit dem Daumen, Zeigefinger und Mittelfinger so ein kartesisches Koordinatensystem (nach) basteln.