Darstellungsformen – Normalform / Scheitelpunktform / Faktorisierte Form
Es gibt mehrere Formen um quadratische Funktionen darzustellen. Wir wollen hier die gebräuchlichsten Vorstellen.
- Die Scheitelpunktform ist die Form, in der man den Scheitelpunkt sehr schnell ablesen kann.
- Die Normalform ist die einfachste Form und der Schreibweise von anderen Funktionen am ähnlichsten.
- Die faktorisierte Form macht es uns sehr leicht die Nullstellen der Funktion zu bestimmen. Allerdings existiert diese Form auch nur wenn die quadratische Funktion auch wirklich Nullstellen hat. Sie wird eher selten eingesetzt.
Die Scheitelpunktform
Die Scheitelpunktform sieht folgendermaßen aus:
![]()
- a: Der Öffnungsfaktor. Dieser sagt ob die Parabel nach oben oder unten geöffnet ist und ob sie gestreckt oder gestaucht ist. (siehe auch Strecken, Stauchen, nach unten geöffnet.
 Die Koordinaten des Scheitelpunkts .
Die Koordinaten des Scheitelpunkts .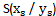
Beispiel 1
![]()
Wir können jetzt sofort den Scheitelpunkt bestimmen. Er liegt bei S(2 / 3). Dabei muss man beachten, dass in der Scheitelpunktform in der Klammer ein Minuszeichen steht. Obwohl in der Klammer -2 steht liegt der Scheitelpunkt also bei +2.
Außerdem können wir sagen, dass die Parabel nach oben geöffnet und in Richtung der y-Achse gestreckt ist.
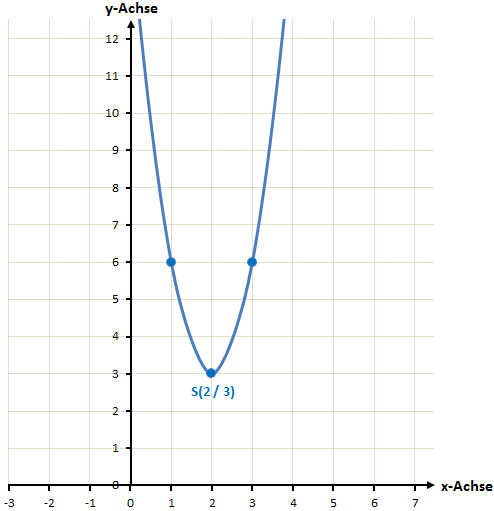
Beispiel 2
![]()
Der Scheitelpunkt liegt bei dieser Funktion bei S(-1 / -4). Wir müssen das Vorzeichen in der Klammer umdrehen um die x-Koordinate des Scheitelpunkts zu erhalten, da in der normalen Scheitelpunktform in der Klammer ein Minuszeichen steht. Man könnte es auch folgendermaßen schreiben:
![]()
Die beiden Minuszeichen werden nun zu einem Pluszeichen, trotzdem ist der Scheitelpunkt bei x = -4.
An dem Vorfaktor a = -1 kann man ablesen, dass Die Parabel außerdem nach unten geöffnet und nicht gestaucht oder gestreckt ist.
Unser Lernvideo zu : Darstellungsformen – Normalform / Scheitelpunktform / Faktorisierte Form
Die Normalform
Die Normalform sieht folgendermaßen aus:
f(x) = ax² + bx + c
- a: Wie bei der Scheitelpunktform ist dies der Faktor der angibt ob die Parabel gestaucht oder gestreckt ist und ob sie nach oben oder nach unten geöffnet ist.
- b: Dieser Faktor gibt die Steigung am y-Achsenabschnitt an. Allerdings ist dieser Wert meistens von eher geringerer Bedeutung.
- c: Gibt den y-Achsenabschnitt an. Also den Punkt an dem die y-Achse geschnitten wird.
Beispiel 1
![]()
Ohne die Funktion zu zeichnen können wir schon einige Aussagen über sie treffen.
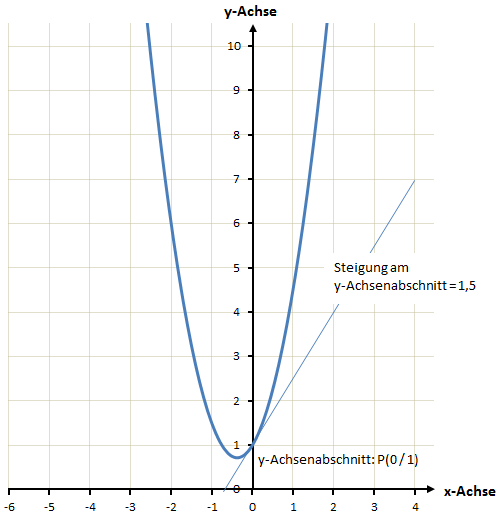
Die Parabel ist nach oben geöffnet und in Richtung der y-Achse gestreckt (2x²).
Die Steigung am Schnittpunkt mit der y-Achse liegt bei 1,5 (1,5x).
Die Parabel schneidet die y-Achse bei y = 1 (+1).
Beispiel 2
![]()
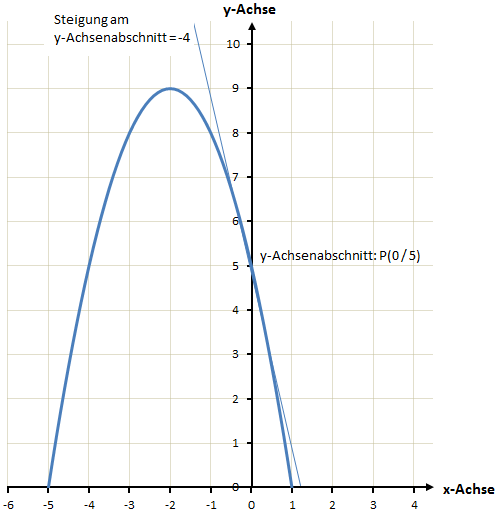
Die Parabel ist nach unten geöffnet und nicht gestaucht oder gestreckt (-x²).
Die Steigung am Schnittpunkt mit der y-Achse liegt bei -4 (-4x).
Die Parabel schneidet die y-Achse bei y = 5 (+5).
Die faktorisierte Form
Die faktorisierte Form existiert nur, wenn die Funktion mindestens eine Nullstelle besitzt. Sie sieht folgendermaßen aus:
![]()
 Die x-Koordinaten der beiden Nullstellen. Sind beide Parameter gleich, gibt es nur eine Nullstelle.
Die x-Koordinaten der beiden Nullstellen. Sind beide Parameter gleich, gibt es nur eine Nullstelle.- a: Wie bei den anderen Formen ist dies der Faktor der angibt ob die Parabel gestaucht oder gestreckt ist und ob sie nach oben oder nach unten geöffnet ist.
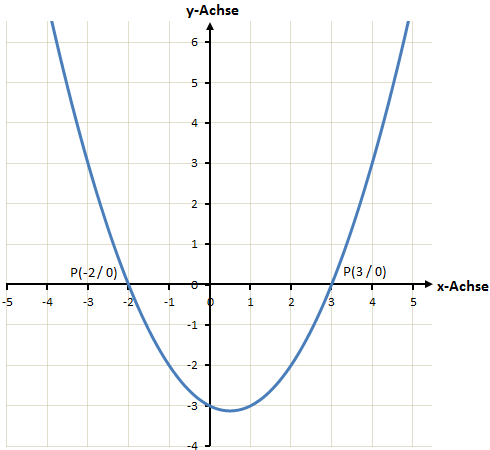
Beispiel
![]()
Die Parabel hat zwei Nullstellen. Die erste liegt bei x = -2 und die zweite bei x = +3. Wir müssen die Vorzeichen umdrehen da in der Originalformel vor den beiden Parametern ![]() und
und ![]() jeweils ein Minuszeichen steht.
jeweils ein Minuszeichen steht.
Die Parabel ist nach oben geöffnet und in Richtung der y-Achse gestaucht.