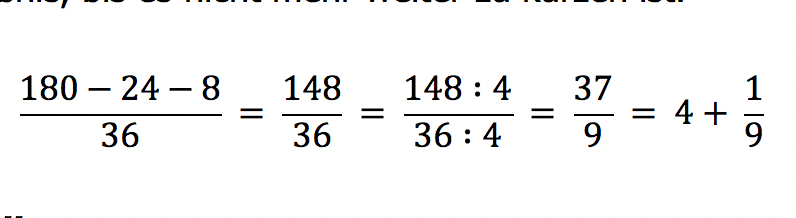Brüche subtrahieren
Das Vorgehen ist fast genau wie bei der Addition:
- Beide Brüche auf denselben Nenner bringen. Hierfür muss zunächst das kleinste gemeinsame Vielfache (kgV) beider Nenner berechnet werden.
- Als nächstes erweitern wir beide Brüche so, dass die Nenner von beiden Brüchen gleich dem berechneten kgV sind.
- Die Zähler der erweiterten Brüche subtrahieren. Das Ergebnis ist der Zähler des Ergebnisbruchs. Der Nenner des Ergebnisbruchs ist gleich den Nennern der erweiterten Brüche.
Unser Lernvideo zu : Brüche subtrahieren
1. Beispiel
![]()
Wir müssen als erstes die beiden Brüche auf einen Nenner bringen. Das kgV von 2 und 4 ist 4. Wir müssen beide Brüche auf einen Nenner von 4 bringen. Der erste Bruch hat bereits einen Nenner von 4. Den zweiten Bruch müssen wir hierfür mit 2 erweitern.
![]()
Jetzt können wir die beiden Zähler einfach subtrahieren:
![]()
Dieser Bruch kann nicht mehr gekürzt werden, deshalb sind wir an dieser Stelle fertig.
2. Beispiel
![]()
Das kgV von 10 und 6 ist 30. Wir müssen also beide Brüche auf einen Nenner von 30 bringen. Dazu erweitern wir den ersten Bruch mit 3 und den zweiten mit 5:
![]()
Da Zähler und Nenner gerade sind, sieht man relativ schnell, dass wir diesen Bruch noch kürzen können. Dazu suchen wir den ggT von 46 und 30. Dieser ist 2. Wir kürzen das Ergebnis also mit 2:
![]()
Brüche subtrahieren – in wenigen Schritten zum Ergebnis
In diesem Kapitel geht es darum, Brüche zu subtrahieren. Das Problem ist, dass Brüche oft einen unterschiedlichen Nenner aufweisen, sodass im ersten Schritt keine Subtraktion möglich ist. Im Vorfeld ist es wichtig, die Brüche auf den gleichen Hauptnenner zu bringen. Für diesen Zweck ist zuerst das kgV zu berechnen oder eine kurze Multiplikation der Nenner durchzuführen. Im zweiten Schritt erweitert der Mathematiker die Zähler, um sie an den neuen Nenner anzupassen. Im dritten Schritt folgt die Subtraktion, was zur gesuchten Lösung führt. Für ein anschaulicheres Ergebnis besteht anschließend die Option, den Bruch zu kürzen.
Brüche auf denselben Nenner bringen
Um Brüche zu subtrahieren, ist es notwendig, beide auf den gleichen Nenner zu bringen. Der Nenner ist der untere Teil des Bruches und benennt die Größe des Bruchteils. Der Zähler oben zählt mit, wie viele Teile des Bruches zur Verfügung stehen. Für das Angleichen der Nenner existieren mehrere Varianten, die zum Ziel führen.
Die erste Methode, die immer funktioniert, ist, beide Nenner miteinander zu multiplizieren. In Abhängigkeit davon, wie groß die Zahlen der Nenner sind, erscheint der Bruch schnell unübersichtlich.
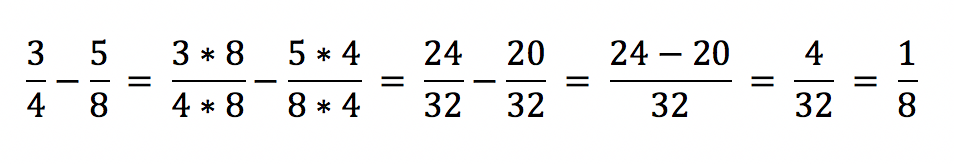
In diesem Beispiel bringen wir die zwei Brüche auf den gemeinsamen Nenner, indem wir 8 * 4 rechnen. Schneller und einfacher geht es, wenn wir in diesem Beispiel auf 8
erweitern. Die Zahl 8
ist in diesem Fall gleichzeitig das kgV von 4
und 8
.
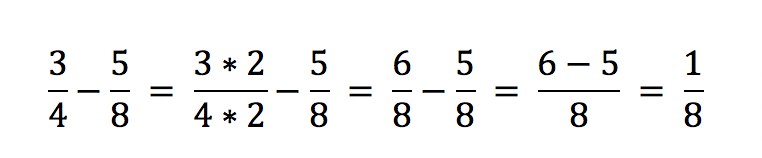
Bei dieser Variante ist im ersten Schritt, das kgV, kleinste gemeinsame Vielfache, zu ermitteln. Im Kapitel „kleinstes gemeinsames Vielfaches“ findet der Leser eine ausführliche Beschreibung und alle notwendigen Informationen über das kgV. Sind die Nenner der Aufgabe zwei- oder mehrstellig, bietet sich die Multiplikation der Brüche nicht mehr an. In einem solchen Fall ist das kgV die richtige Lösung.
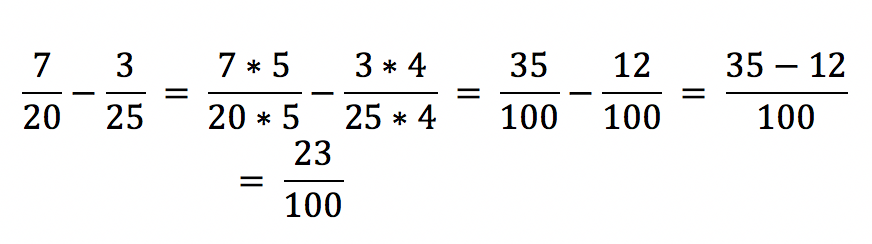
In diesem Beispiel ergibt eine Multiplikation der Nenner 500, das kgV von 20
und 25 ist 100
. Immer wenn der Anwender zuerst die Nenner multipliziert, ist für das Endergebnis eine Kürzung notwendig. Zusätzlich rechnet dieser mit höheren Zahlen, wobei sich schneller Fehler einschleichen. Die Variante mit der Berechnung des kgV ist übersichtlicher.
Zweiter Schritt – Zähler erweitern
Es spielt keine Rolle, welchen ersten Schritt der Mathematiker wählt, bei beiden Varianten ist es notwendig, die Zähler zu erweitern. Würde der Anwender das Erweitern weglassen, wäre das Ergebnis nicht gleich der Aufgabe. Wenn ich ein viertel Stück Kuchen von einem halben Stück subtrahieren möchte, ist vorher das eine halbe Stück in zwei Viertel zu teilen. Anschließend ergibt zwei Viertel minus einem Viertel ein Viertel. Ohne diese Erweiterung des Zählers würde der Anwender ein Viertel minus ein Viertel rechnen, sodass nichts übrigbliebe.
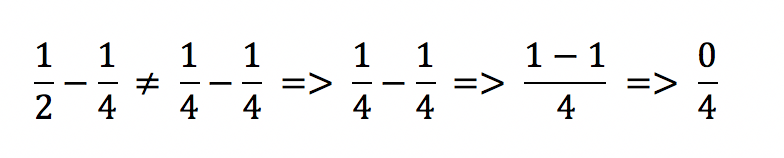
sondern
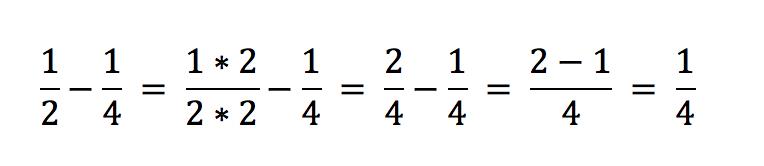
Weitere Beispiele:

Um diese Brüche zu subtrahieren, wählt der Mathematiker den Hauptnenner 8. Für diesen Zweck ist es wichtig, den Bruch 3/4 auf den gleichen Nenner zu bringen. In diesem Schritt erweitert der Anwender den Bruch um den Faktor 2.
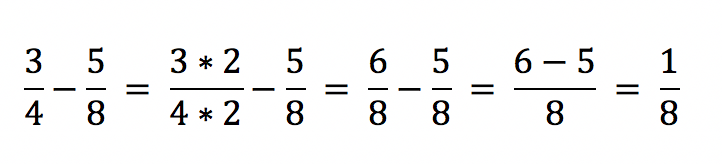
In diesem Beispiel sind die Brüche Siebenzwanzigstel und Dreifünfundzwanzigstel zu subtrahieren. Für diesen Zweck bringt der Mathematiker die Brüche auf einen gemeinsamen Nenner dem kgV 100. Der erste Bruch ist somit mit dem Faktor 5 zu erweitern und der zweite mit dem Faktor 4. Aus den Zählern 7 und 3 ergeben sich neue Zähler 35 und 12.
Dritter Schritt – Brüche subtrahieren
Der dritte Schritt, um Brüche zu subtrahieren, ist, eine einfache Subtraktion durchzuführen. Vor diesem Schritt erledigt der Anwender das Bestimmen eines gleichen Hauptnenners und die Erweiterung des Zählers. Anschließend stehen sich neben dem Minuszeichen zwei Brüche mit demselben Nenner gegenüber. An dieser Stelle ist es erlaubt, eine einfache Subtraktion durchzuführen. Für diesen Zweck subtrahiert der Mathematiker die beiden Zähler und erhält die gesuchte Lösung.
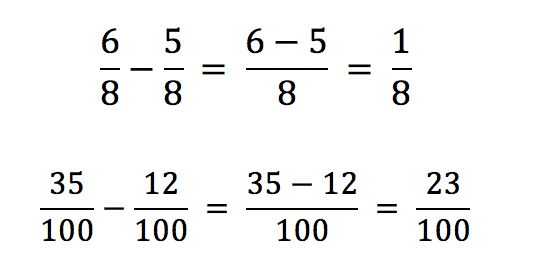
Letzter Schritt – Brüche kürzen
Im letzten Schritt folgt das Verbessern des erhaltenen Ergebnisses. Nicht immer ist es notwendig, Brüche zu kürzen, weil oft kein gemeinsamer Faktor zur Verfügung steht. Gerade zweistellige Zahlen sind immer zu kürzen, wobei ungerade Zahlen weniger oft zu vereinfachen sind.
Bei diesem Vorgang nimmt der Anwender das vorläufige Ergebnis eines Bruches her und analysiert es. Ist es möglich, Nenner und Zähler durch einen gemeinsamen Dividenden zu teilen, nennt sich dieser Schritt „Kürzen“.

Mehrere Brüche mit unterschiedlichen Nennern subtrahieren
Im zweiten Schritt ist es notwendig, alle Brüche mit dem jeweiligen Faktor zu erweitern. An dieser Stelle erweitert der Mathematiker den Zähler, sodass sich der Bruch nicht verkleinert. Sind alle Brüche auf dem gleichen Nenner und alle Zähler ausreichend erweitert, folgt eine einfache Subtraktion der Zähler als dritten Schritt. Wenn es möglich ist, das Ergebnis weiter zu vereinfachen, kürzt der Anwender den Bruch.
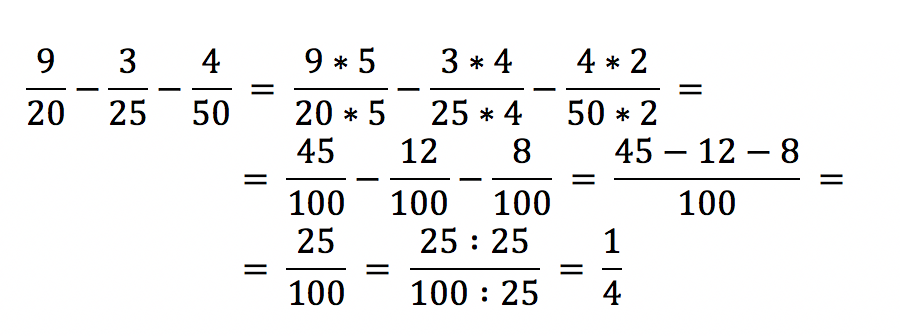
Ganze Zahlen mit Brüche subtrahieren
Eine weitere Aufgabe ist es, ganze Zahlen mit Brüche zu subtrahieren. Für diesen Zweck existieren zwei Varianten. In der einen Variante löst der Mathematiker den gegebenen Bruch zuerst auf. Ein Bruch ist gleichbedeutend einer Division, die in einer Klammer steht. Das Ergebnis des Bruches rechnet der Anwender anschließend gegen die ganze Zahl.
Die andere Methode ist es, die ganze Zahl als Bruch darzustellen. Eine natürliche Zahl a ist das Gleiche wie a/1. Anschließend folgen die normalen Schritte, mit der Brüche zu subtrahieren sind. Im ersten Schritt bestimmen wir den Hauptnenner, der in der Regel der des ursprünglichen Bruches ist. Im nächsten Schritt erweitern wir a um den gewählten Nenner. Im letzten Schritt subtrahieren wir den ersten minus den zweiten Bruch und erhalten das gesuchte Ergebnis.
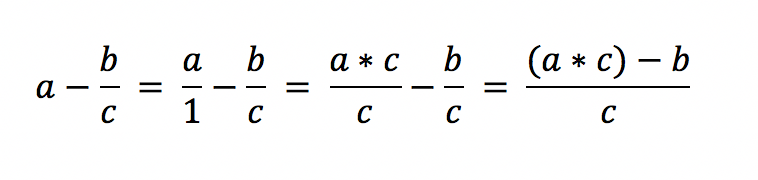
Als Beispiel mit Zahlen folgt eine kleine Aufgabe mit Musterlösung:
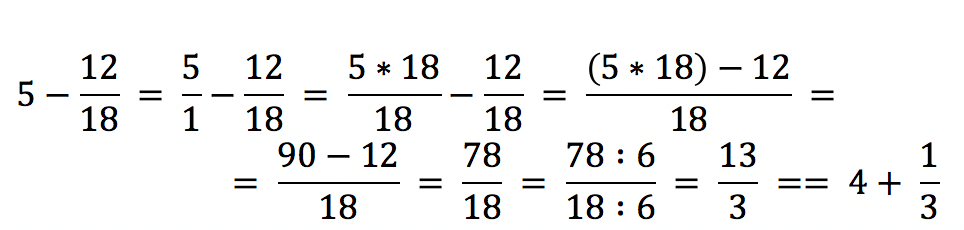
Abschließendes Beispiel mit mehreren Brüchen und ganzen Zahlen
In diesem Beispiel vereinen wir alles Gelernte in einer konkreten Aufgabe. Als Aufgabenstellung haben wir:
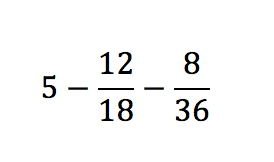
Im ersten Schritt ermitteln wir einen gemeinsamen Nenner, den wir als Hauptnenner 36 bestimmen. Im gleichen Zug wandeln wir die Zahl 5
in einen Bruch um.
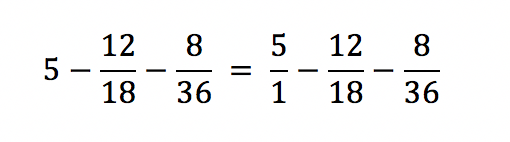
Um diesen Ausdruck auf einen gemeinsamen Nenner zu bringen, ist es notwendig, die Zähler zu erweitern.
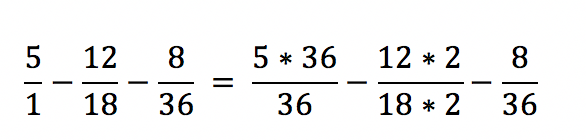
Im dritten Schritt vereinfachen wir die Gesamtrechnung, bis ausschließlich Minuszeichen über dem Bruchzeichen zu sehen sind.
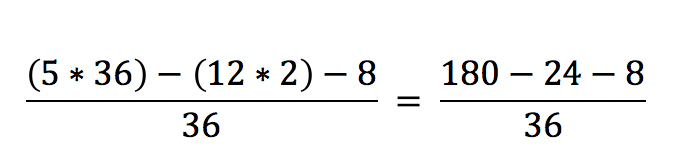
Jetzt erkennen wir eine einfache Minusrechnung der Zähler. Nach diesem Schritt vereinfachen wir das Ergebnis, bis es nicht mehr weiter zu kürzen ist.