Mehrstufige Zufallsexperimente
Etwas komplizierter wird es, wenn das Experiment, von dem wir die Wahrscheinlichkeit bestimmen wollen mehrstufig ist. Man nennt dies ein mehrstufiges Zufallsexperiment.
In diesem Fall müssen wir ein Baumdiagramm benutzen. Dieses hilft uns die verschiedenen Möglichkeiten zu visualisieren und erleichtert uns auch das Berechnen der Wahrscheinlichkeiten.
Unser Lernvideo zu : Mehrstufige Zufallsexperimente
Beispiel 1
Als Beispiel nehmen wir das werfen einer Münze. Wir werfen die Münze 2-mal. Hierfür zeichnen wir zunächst das entsprechende Baumdiagramm. Die Wahrscheinlichkeit ist bei einer normalen Münze für Kopf oder Zahl 50%.
Wir beginnen mit dem ersten Wurf:
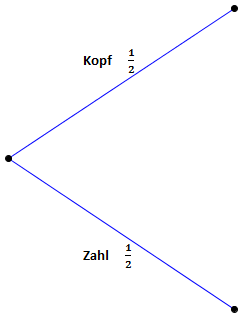
Wir haben links unseren Startpunkt. Die jeweiligen Wahrscheinlichkeiten für einen Pfad schreibt man immer direkt an den Pfad. Die Wahrscheinlichkeit für Kopf ist also 50%. Wir können vom Startpunkt also entweder dem oberen oder dem unteren Pfad folgen.
Nun folgt der zweite Wurf:
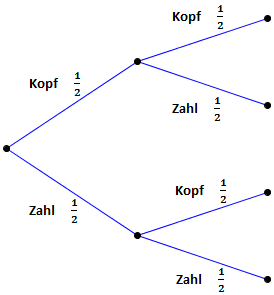
Wir fügen also an alle Pfade noch den zweiten Wurf an. Dieser kann natürlich auch wieder mit Kopf oder Zahl ausgehen. Auch hier notieren wie wieder die Wahrscheinlichkeiten.
Wir berechnen nun die Wahrscheinlichkeit eines Ergebnisses indem wir die entsprechenden Pfade des Baumdiagramms entlang gehen und die Wahrscheinlichkeiten der benutzen Zweige multiplizieren. Wenn wir zum Beispiel die Wahrscheinlichkeit berechnen wollen, dass erst Kopf und dann Zahl geworfen wird, folgen wir dem markierten Pfad:
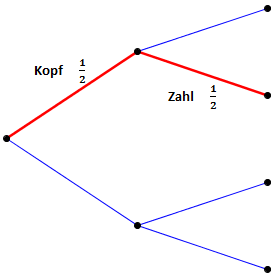
Um die Gesamtwahrscheinlichkeit für dieses Ereignis zu berechnen, müssen wir die einzelnen Wahrscheinlichkeiten multiplizieren:
![]()
Die Wahrscheinlichkeit beträgt für dieses Ereignis 25%.
Wir berechnen nun auch die Wahrscheinlichkeiten der anderen Pfade.
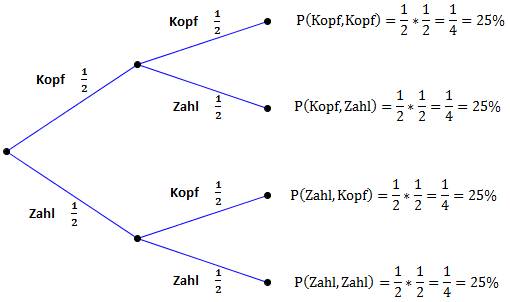
Natürlich sind auch hier alle Wahrscheinlichkeiten gleich groß.
Wenn wir nun berechnen möchten wie Wahrscheinlich es ist, dass wir bei den beiden würfen einmal Kopf und einmal Zahl werfen (Reihenfolge egal), müssen wir alle Ergebnisse addieren die diesem Ereignis entsprechen.
Wir addieren also die Wahrscheinlichkeit des Pfads P(Kopf, Zahl) und des Pfads P(Zahl, Kopf). Wir erhalten also eine Warhscheinlichkeit von
P(E) = P(Kopf, Zahl) + P(Zahl, Kopf) = 25% + 25% = 50%.
In der hälfte der Male erhalten wir demnach bei zwei würfen einmal Zahl und einmal Kopf.
Beispiel 2
In einem Krug sind 15 orange 10 rote und 3 blaue Kugeln. Wir ziehen drei-mal hintereinander. Die Kugeln die wir ziehen behalten wir und legen sie nicht in den Krug zurück. Wie groß ist die Wahrscheinlichkeit, dass wir genau zwei rote Kugeln ziehen? (Die dritte Kugel kann also entweder blau oder orange sein)
Um diese Frage zu beantworten zeichnen wir zunächst wieder das Baumdiagramm. Wir beginnen mit dem ersten Zug.
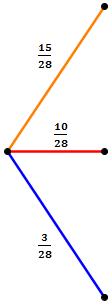
Wir haben also drei Möglichkeiten für die drei Farben. Jeder Farbe hat eine andere Wahrscheinlichkeit, da sie unterschiedlich oft im Krug enthalten ist. Es ist also deutlich wahrscheinlicher, dass wir eine orange Kugel ziehen als dass wir eine blaue ziehen. Um die jeweilige Wahrscheinlichkeit zu erhalten teilen wir die Anzahl der Kugeln der jeweiligen Farbe durch die Gesamtzahl der Kugeln die sich noch im Krug befinden.
Nun folgt der zweite Wurf:
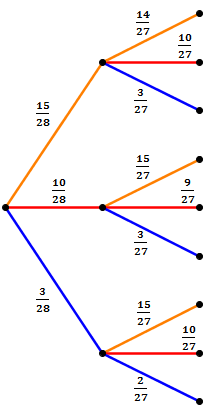
Wir müssen bei den Wahrscheinlichkeiten beachten, dass jetzt natürlich eine Kugel weniger im Krug ist, da wir schon eine gezogen haben. Bei dem obersten Pfad beispielsweise wurde im ersten Zug eine orangene Kugel gezogen. Beim zweiten Zug sind dadurch nur noch 14 orangene Kugeln im Krug. Insgesamt sind noch 27 Kugeln im Krug vorhanden.
Es folgt der dritte Zug:
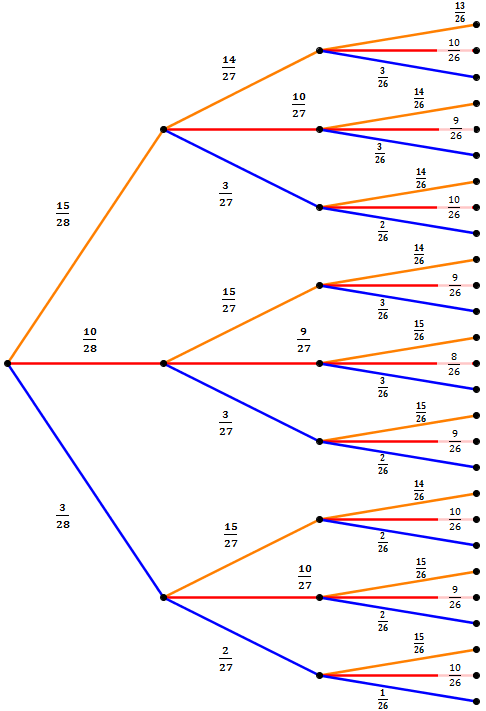
Wir sehen sofort, dass es jetzt schon etwas komplexer wird. Das Prinzip ist aber genau das gleiche. Wir sind nun also fertig mit dem Baumdiaramm und müssen uns nun die für uns relevanten Pfade raussuchen. Wir möchten die Wahrscheinlichkeit für das Ereignis berechnen, dass genau zwei rote Kugeln gezogen werden. Wir markieren zunächst alle Pfade wo das der Fall ist.
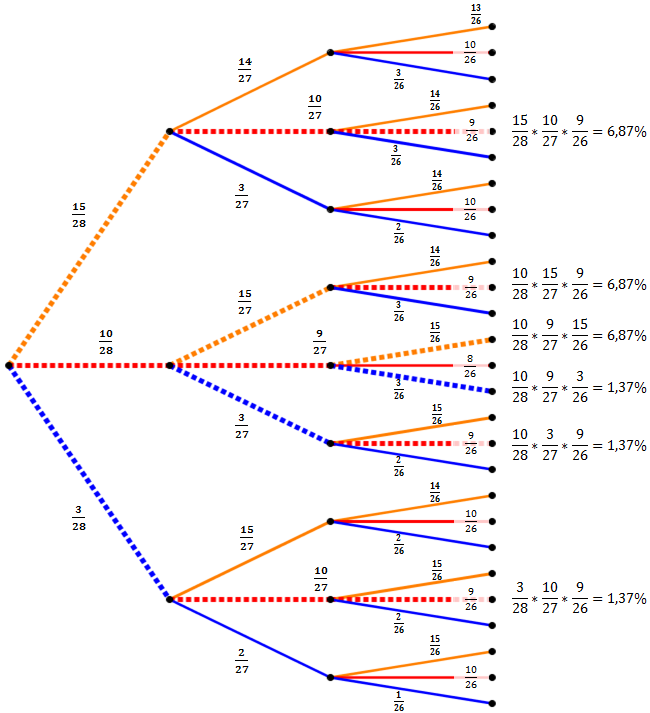
Neben jedem relevanten Pfad haben wir nun die Wahrscheinlichkeit notiert. Dazu müssen wir die einzelnen Pfade multiplizieren. Jetzt müssen wir nur noch alle Wahrscheinlichkeiten addieren und erhalten die Gesamtwahrscheinlichkeit für das Ereignis:
![]()
Die Wahrscheinlichkeit, dass genau 2 rote Kugeln gezogen werden beträgt also 24,72%. Ungefähr bei jedem vierten Zug ziehen wir also 2 rote Kugeln.
