Darstellungsformen für Ebenen
Es gibt drei gängige Darstellungsformen für Ebenen.
- Die Parameterform
- Die Koordinatenform
- Die Normalenform
Bisher haben wir die Parameterform kennengelernt. Deshalb werden wir die Koordinaten- und die Normalform hier vorstellen.
Unser Lernvideo zu : Darstellungsformen für Ebenen
Die Koordinatenform
Die Koordinatenform sieht folgendermaßen aus:
![]()
x, y und z sind dabei die Koordinaten der Ebene im Koordinatensystem. a, b, c und d sind die Parameter die die Lage und Ausrichtung der Ebene beschreiben. Alle Kombinationen von x, y und z welche die Gleichung lösen, sind Punkte auf der beschriebenen Ebene.
Beispiel
![]()
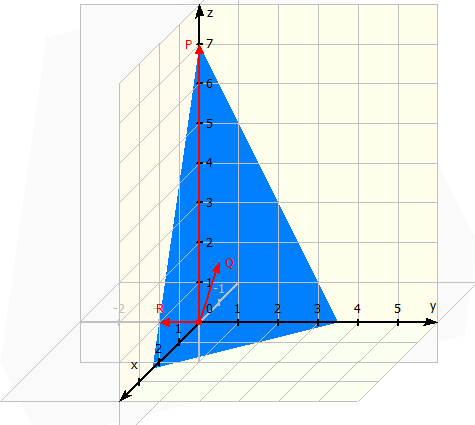
Beispiele für Punkte die auf der Ebene liegen sind zum Beispiel:
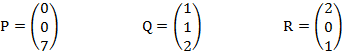
Alle diese Punkte erfüllen die Gleichung und liegen deshalb auf der beschriebenen Ebene.
Die Normalenform
Die Normalenform (oder auch Normalform) ist eine gängige Darstellungsform für Ebenen. Der Vorteil ist hier, dass man die Normale der Ebene direkt ablesen kann und die Normale oft für weitere Berechnungen benötigt wird.
Die Normalenform sieht folgendermaßen aus:
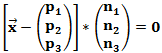
![]() ist dabei die Ebene,
ist dabei die Ebene, ![]() ist der Ortvektor (oder auch Stützvektor genannt) und
ist der Ortvektor (oder auch Stützvektor genannt) und ![]() ist der Normalenvektor, welcher senkrecht auf der Ebene steht.
ist der Normalenvektor, welcher senkrecht auf der Ebene steht.
Umrechnung der Darstellungsformen
Oft ist es wichtig, dass man die Darstellungsformen ineinander überführen kann. Dazu muss man wissen wie man die benötigten Werte berechnen kann. In den folgenden Kapiteln zeigen wir alle benötigten Umrechnungen.
