Umfang einer Raute
Hier findest du die Erklärung zur Berechnung des Umfangs einer Raute.
Um von dieser geometrischen Figur den Umfang zu ermitteln, muss man sie kennen.
Zur Wiederholung:
Eine Raute ist ein Viereck mit vier Ecken und vier Seiten. Die gegenüberliegenden Winkelgrößen sind lgeich groß und ergeben insgesamt 360°. Die Seiten sind alle gleich lang.
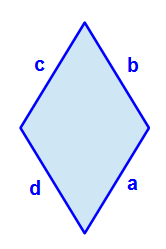
Die Abbildung zeigt eine allgemeine Raute mit den angegebenen Seitenbezeichnungen a, b, c und d. Da alle Seiten einer Raute gleich lang sind, können wir die Seitenbezeichnung dementsprechend angleichen.
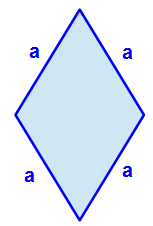
So ist die Raute korrekt beschriftet. Wir nutzen im Allgemeinen die Bezeichnung a als Seite. Dies ist aber variabel.
Lerntool zu Umfang einer Raute
Unser Lernvideo zu : Umfang einer Raute
Die Formel des Umfangs
Schritt für Schritt werden wir an einem Beispiel die Formel zur Berechnung des Umfangs einer Raute ermitteln.
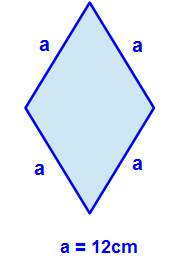
Wir betrachten unsere gegebene Raute. Sie soll die Seitenlänge a = 12cm haben. Um den Umfang zu berechnen, können wir alle Seiten einzeln miteinander addieren.
Allgemein geschrieben wäre das: U = a + a + a + a = 4•a
Im Beispiel: U = 12cm + 12cm + 12cm + 12cm = 4•12cm = 48cm
Somit haben wir die Formel zur Berechnung des Umfangs ermittel:
![]()
Wie vielleicht auffällt, ist die Formel für die Raute identisch zur Formel des Quadrats. Dies liegt daran, dass sowohl beim Quadrat als auch bei der Raute die Seiten alle gleich lang sind. Der Unterschied der Figuren ist, dass in einem Quadrat die Winkel immer 90° sind. In einer Raute sind nur die sich gegenüberliegenden Winkel identisch, müssen aber nicht 90° sein.
Zum Verständnis: Jede Raute ist ein Quadrat, aber nicht jedes Quadrat ist eine Raute!
Beispiel 1
Wir berechnen den Umfang einer Raute mit der Seitenlänge a = 8cm:
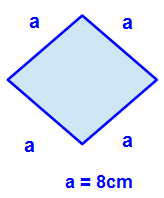
Wir berechnen wie wir es bisher auch gehandhabt haben, indem wir uns notieren, was ist gegeben, was gesucht und danach setzen wir ein.
Gegeben: a = 8 cm
Gesucht: U
Formel: U = 4a
Einsetzen und berechnen: U = 4•8cm = 32cm
Antwort: Der Umfang der Raute ist U = 32cm.
Beispiel 2
Nun berechnen wir nicht den Umfang einer Raute, sondern wir haben diesen schon gegeben und möchten die Seitenlänge der Raute ermitteln.
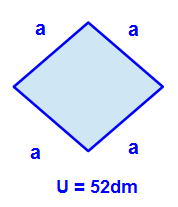
Die Raute soll einen Umfang von 52dm haben. Auch diesen ermitteln wir mit der uns bekannten Formel:
Gegeben: U = 52 dm
Gesucht: a
Formel: U = 4a
Umstellen der Formel nach a:
U = 4•a | :4
U/4 = a
Einsetzen und berechnen: a = U/4 = 52cm / 4 = 13cm
Antwort: Die Seitenlänge a beträgt 13cm.
