sin x Ableitung
Eigenschaften der Sinusfunktion
- Die Ableitung der Kosinusfunktion ist die negative Sinusfunktion, ihre Stammfunktion ist die positive Sinusfunktion
- Monotonieverhalten: Zwischen den Extrema ist die Funktion jeweils monoton steigend bzw fallend
- Die Sinusfunktion ist eine ungerade Funktion, d.h ihr Graph liegt punktsymmetrisch zum Ursprung des Koordinatensystems
Wofür braucht man die Ableitung
►Eine Ableitung hilft dir, die Steigung eines Graphen an einer beliebigen x-Koordinate zu bestimmen.
►Du bildest die Ableitung und setzt in diese dann den x-Wert ein. Das „Ergebnis“ ist die Steigung.
Sinus Ableiten
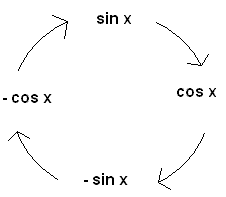
Stellt euch eine Uhr vor. Dann wird das Ableiten nicht so schwer sein. Nach dem Uhrzeiger Sinn müsst ihr vorgehen und dementsprechend Ableiten.
Wenn sin (x) abgeleitet wird so ergibt das cos(x). Wird cos(x) abgeleitet ist das Ergebnis -sin(x). Die Ableitung von -sin(x) ist -cos(x). Wird -cos(x) abgeleitet wird, so ist das Ergebnis wieder sin(x).
Die richtige Regel anwenden
- Ihr müsst immer die Kettenregel benutzen. Die Kettenregel braucht man immer dann, wenn man es nicht mehr nur mit den „Grundfunktionen“ zu tun hat, sondern wenn statt des einzelnen x ein erweiterter Ausdruck steht. Schon ein einfaches Minus stellt in diesem Sinne eine Erweiterung dar bsp 2*(sin) → -2(sin)
►Bei der Kettenregel wird die äußere Funktion zuerst abgeleitet und mit der inneren Ableitung multipliziert.
![]()
Beispiele
f(x)= sin (2x-π) Lösung ► 2cos (2x -π)
f(x)= 2 cos( π/2x +1) Lösung ►-π* sin(π/2x+1)
oder
y= 6sin (4x)
►Substitution u= 4x
►Äußere Funktion= 6sin(u)
►Äußere Ableitung= 6cos(u)
►Innere Funktion= 4x
►innere Ableitung= 4
►y` = 4*6cos (u)
►y`= 24cos (4x)
