Zentrische Streckung I
Unter einer zentrischen Streckung versteht man eine Abbildung mit einem Streckfaktor k von einem Ursprungsbild. So wird von einem Streckzentrum Z ein Punkt um den Streckfaktor k neu abgebildet. Der Faktor bestimmt, ob die Abbildung größer oder kleiner wird und in welcher Richtung die Abbildung liegt.
Z = Streckzentrum
k = Streckfaktor
wenn k > 1, dann ist die Abbildung vergrößert
wenn k < 0, dann liegt das Streckzentrum zwischen den Abbildungen
wenn 0 < k < 1, dann wird die Abbildung verkleinert
Die Winkelgrößen bleiben erhalten und die neuen Geraden sind parallel zu den Ursprungsgeraden.
Das Ursprungsbild, kann sowohl eine geometrische Figur als auch eine Streckue oder ein Punkt sein. Die Streckung kann man in jedem Fall durchführen.
Dieses sind die allgemeinen Informationen zur Zentrischen Streckung. Nun schauen wir uns dieses genauer an.
Unser Lernvideo zu : Zentrische Streckung I
Vergrößerte Abbildung
Als erstes betrachten wir den Umstand der Vergrößerung. dabei ist der Streckfaktor k > 1. Das zeigt uns, dass die Abbildung größer sein wird als das Ursprungsbild und dass die neue Abbildung auf der selben Seite des Streckzentrums liegt, wie das Ursprungsbild. In unserem Beispiel nutzen wir ein beliebiges Dreieck und beliebiges Z und k = 2.
1. Schritt: Zeichnen des Bildes und des Streckzentrums Z
Als erstes wird das zu streckende Bild gezeichnet und auch das Streckzentrum Z. Ganz nach Aufgabenstellung, kann es klar bestimmt, z.B. in einem Koordinatensystem oder auch frei wählbar sein.
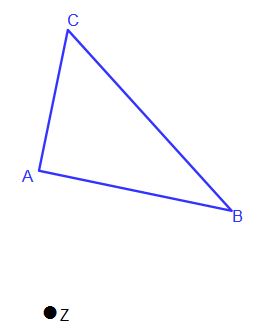
In unserem Beispiel haben wir ein blaues Ursprungsdreieck gewählt und auch das Streckzentrum Z ist beliebig eingesetzt.
2. Schritt: Einzeichnen der Geraden ZA, ZB und ZC
Da k = 2 in unserem Beispiel wissen wir, dass die neue Abbildung auf der selben Seite liegen wird, wie die Ursprungsabbildung und dass sie größer sein wird. Daher zeichnen wir nun Hilfsgeraden von Z zu A, Z zu B und Z zu C.
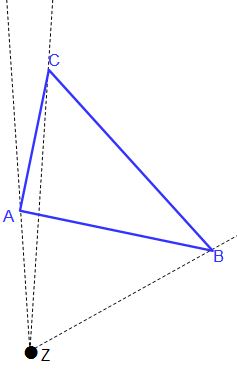
Wir sehen, dass nun vom Streckzentrum Z zu den einzelnen Eckpunkten Hilfslinien genzeichnet wurde und auch darüber hinaus. Diese Vorbereitung benötigen wir für den nächsten Schritt.
3. Schritt: Einzeichnen des Streckfaktors
Nun zeichnen wir den Streckfaktor k ein. In unserem Beispiel ist k = 2. Das bedeutet, dass die Strecke ZA‘ zweimal so lang ist wie ZA. Dazu messen wir zunächst die Strecke ZA.
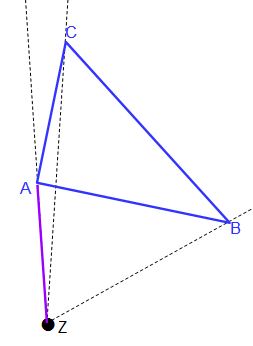
Die violette Linie zeigt uns die zu messene Strecke ZA. Diese könnt ihr mit dem Linial ausmessen oder genauer mit dem Zirkel die Entfernung einstellen.
In unserem Beispiel ist k = 2, somit müssen wir nun die Entfernung zu Z verdoppeln. Dazu messen wir die doppelte Strecke auf der Hilfslinie ab und haben dort unseren Abbildungspunkt A‘ definiert.
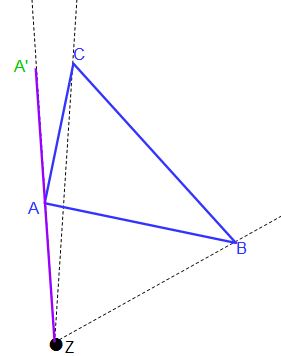
Wieder seht ihr die violette Linie. Sie verläuft auf der Hilfsgeraden ZA und ist nun doppelt so lang wie die Strecke ZA. Dieses könnt ihr am besten mit dem Zirkel abmessen, dass ist am genauesten und auch am schnellsten. Dort wo die violette Linie endet, ist mei neuer Punkt A‘.
4. Schritt: Einzeichnen aller Abbildungspunkte
Als nächsten werden auch die Punkte B‘ und C‘ auf die selbe Weise ermittelt und dann verbunden.
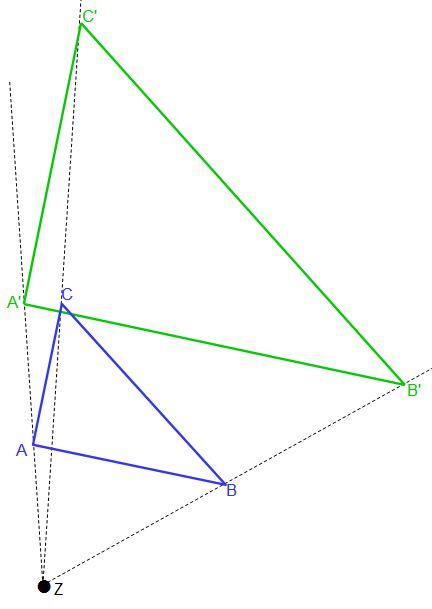
Nun seht ihr das Endergebnis. Alle Punkte wurden wie in Schritt 3 ermittelt und dann zusammengeführt. Das neue grüne Dreieck hat den Streckfaktor k = 2. Die abgebildeten Linien sind parallel zu ihren Ursprungslinien, d.h. AB ist parallel zu A’B‘. Auch die Winkel des neuen Dreiecks haben die selben größen.
Somit haben wir den ersten der drei Teile einer zentrischen Streckung kennen gelernt.
Verkleinerte Abbildung
Als nächsten schauen wir uns an, was bei einer Verkleinerung passiert. Auch wenn es kleiner wird, nennt man es trotzdem Zentrische Streckung. Bei einer Verkleinerung liegt der Streckfaktor k zwischen 0 und 1. In unserem Beispiel nehmen wir k = 0,5. Das heißt die Strecke von Z zu den Eckpunkten ist 0,5 mal so lang.
1. Schritt: Zeichnen des Bildes und des Streckzentrums.
Als erstes zeichnet ihr euer zu streckendes Bild und das Streckzentrum ein. Dies kann definiert sein oder frei wählbar.
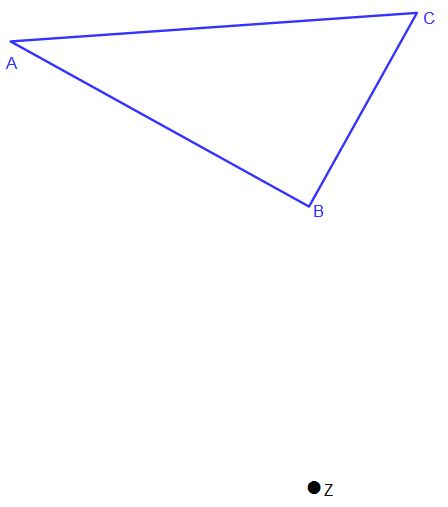
In unserem Beispiel seht ihr wieder ein beliebiges Dreieck und auch ein frei gewähltes Streckzentrum Z.
2. Schritt: Einzeichnen der Hilfsgeraden
Als nächstes zeichnet ihr die Hilfsgeraden ZA, ZB und ZC ein.
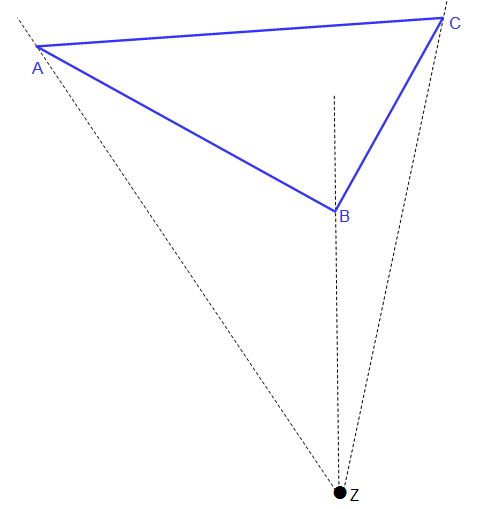
3. Schritt: Einzeichnen des Streckfaktors
Als nächstes folgt wieder das einzeichnen des Streckfaktors. Dazu messt ihr zunächst die Strecke ZA aus.
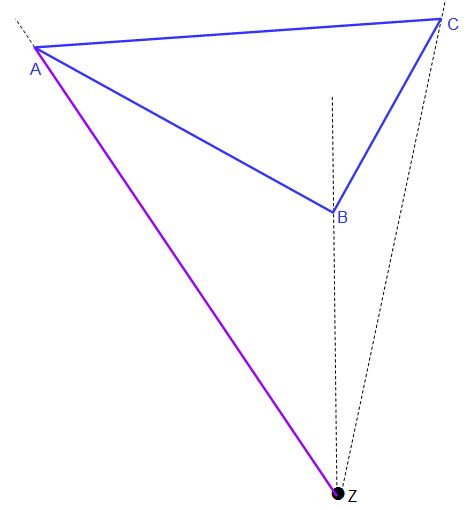
Die violette Linie zeigt euch die Strecke ZA. Diese wird nun mit dem Streckfaktor k multiplizert. Das Ergebnis zeigt an wie lang ZA‘ ist.
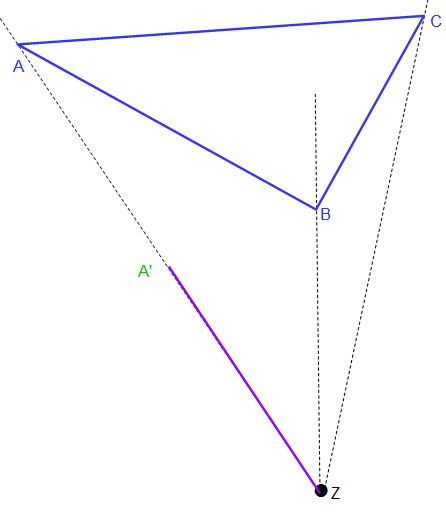
In der obigen Abbildung seht ihr nun die verkürzte violette Linie. Da unser Streckfaktor im Beispiel k = 0,5 ist, ist die Strecke ZA‘ halb so lang wie ZA.
4. Schritt: Einzeichnen aller Abbildungspunkte
Nun zeichnen wir wie in Schritt 3 alle anderen Abbildungspunkte ein und nehmen dazu jeweils den Streckfaktor k = 0,5. Danach verbinden wir die Abbildungspunkte miteinander.
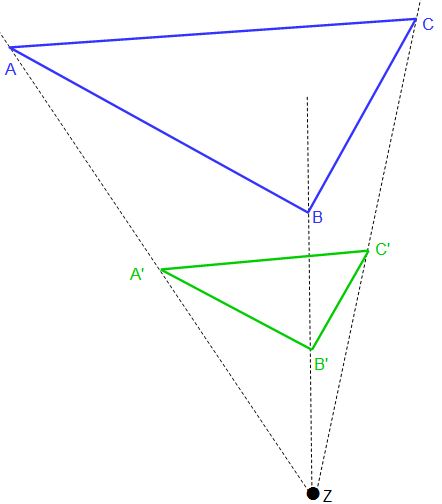
In unserer Abbildung seht ihr nun das neue grüne Dreieck mit den Punkten A‘, B‘ und C‘. Die Strecken vom Streckzentrum zu den Abbildungspunkten sind halb so lang wie die Strecken vom Zentrum zu den Ursprungspunkten, da in unserem Beispiel k = 0,5 ist. Die Strecken sind parallel zu einander, d.h, dass AB parallel zu A’B‘ ist usw. Auch die Winkel des neuen Dreiecks sind genauso groß wie die des Ursprungsdreiecks.
Nun kennt ihr die Vorgehensweise der Vergrößerung und er Verkleinerung mit einer Zentrischen Streckung. Auf der nächsten Seite zeigen wir euch, wie wir verfahren, wenn k < 0 ist.
